使用场景：解决分类问题
- Logistic Regression使用场景是解决分类问题
- 二分类或者多分类,多分类模型(多次二分类或者后面学习到的softmax)
- 数据分布
- 二分类模型中，线性分布：
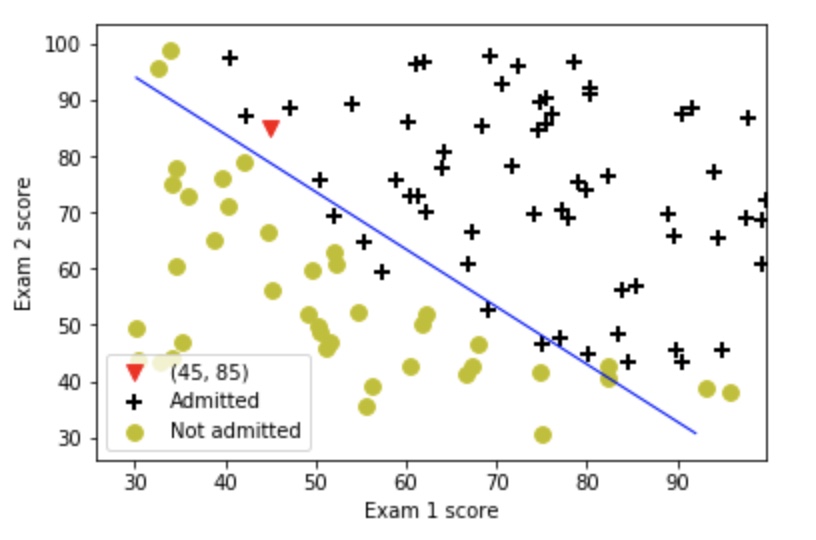
- 也可能是非线性分布：
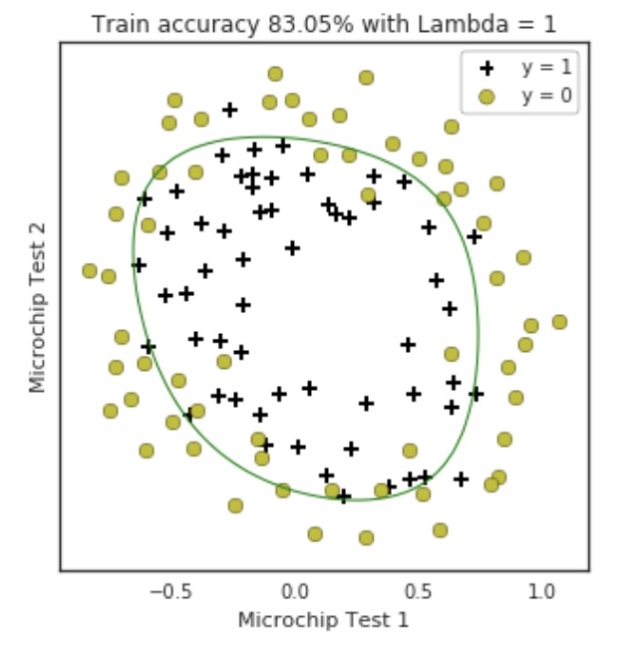
- 二分类模型中，线性分布：
逻辑回归模型
- Hypothese：$h_\theta(x)=g(z)=\frac{1}{1+e^{-z}}$
Sigmoid: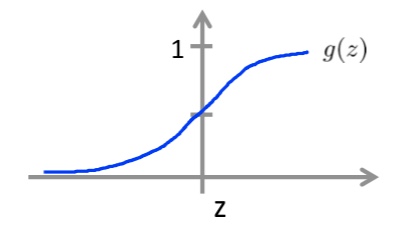
所以：$y = \begin{bmatrix}
1(h_\theta(x) >= 0.5)
\
0(h_\theta(x) < 0.5)
\end{bmatrix}$ - $z = \begin{bmatrix}
\theta^Tx = \theta_0+\theta_1x_1+\theta_2x_2…(数据线性分布)
\
x^2+y^2-1 (非线性分布，这里是圆形分布)
\end{bmatrix}$ - Cost fun:
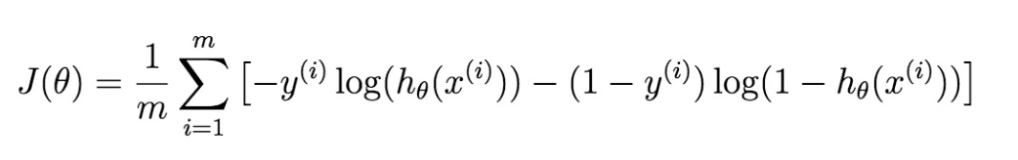
- 推导：
- 推导：
- 梯度：
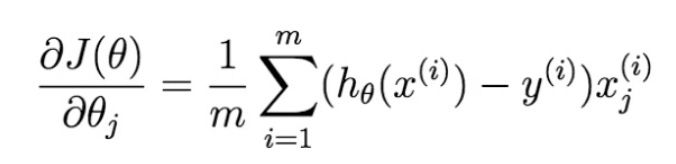
条件概率角度理解
- $h_\theta(x) = P(y=1|x;\theta) = 1-P(y=0|x;\theta)$
- $P(y=1|x;\theta) + P(y=0|x;\theta) = 1$
正则化
- 当数据分布为非线性的时候，如果使用多项式去拟合，那么很容易出现过拟合问题，这个时候就需要使用L1，L2正则化去处理
- 直观理解：正则化的根本目的就是将过拟合的参数调到合适大小
- cost_reg:
- 梯度_reg:
- 超参数$\lambda$对拟合程度和准确率等的影响
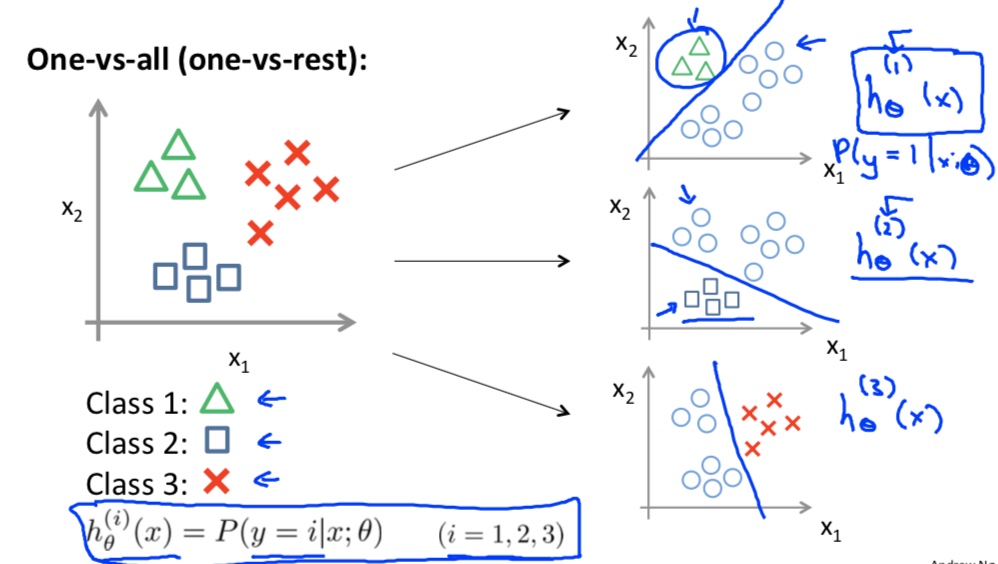
多分类
- 思想：对每个类别都会有一个$h_\theta(x)$对应：$h_\theta^i(x)$。输入x，获取使最大的$h_\theta^i(x)$的i值
