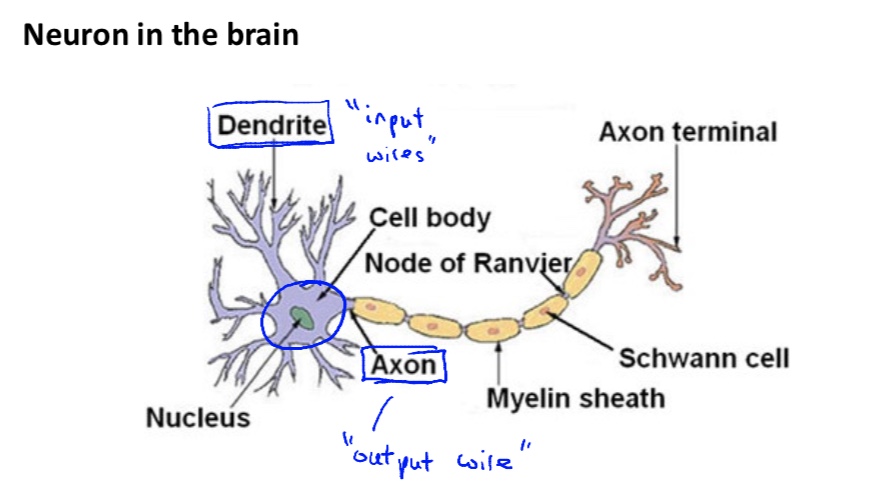
人脑神经元
- 人脑内就有很多神经元构成,神经元与神经元之间互相连接,传递电信号等
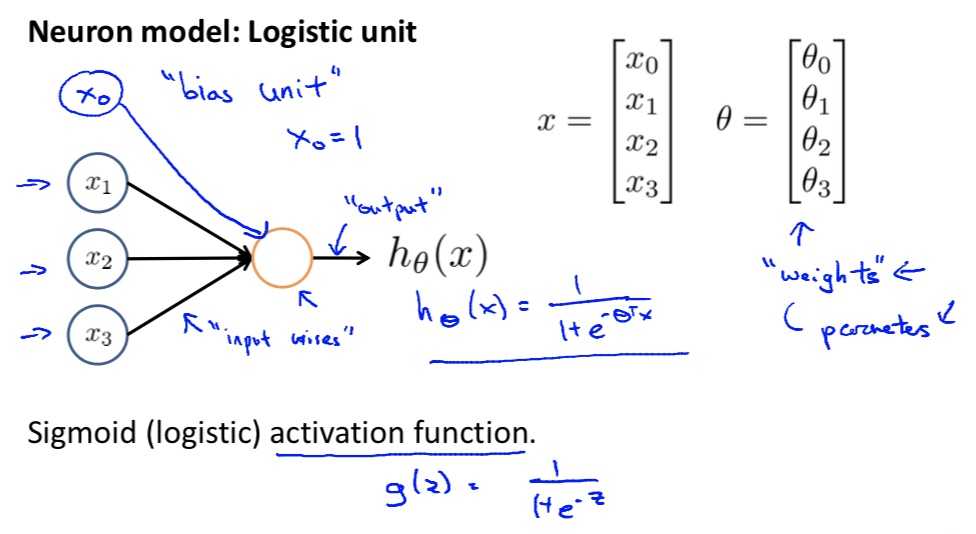
模型
- 基础结构:类似逻辑回归模型
网络架构
- 每个神经单元都是一个上图的基础结构,输出a是激活值,g是sigmoid激活函数
- 架构分为第一层(输入层),第二层(隐藏层)….输出层
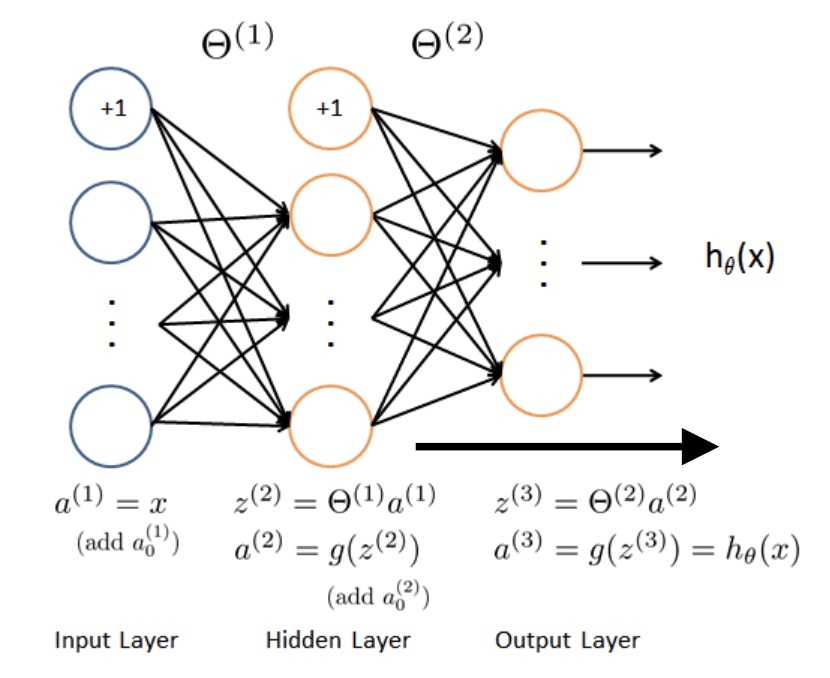
- 前向计算:每个神经元都依次计算

直观理解网络含义
- 每一层都是通过逻辑回归来完成,通过增加隐层的数量,或者通过增加一个隐藏中的单元数,来完成不同的功能,就能够得到更复杂的模型,完成更复杂的功能(简单理解为每个神经单位都是一个逻辑回归结构,都能够完成一个独立的功能)
- 比如亦或问题

- 比如亦或问题
- 每一层都是通过逻辑回归来完成,通过增加隐层的数量,或者通过增加一个隐藏中的单元数,来完成不同的功能,就能够得到更复杂的模型,完成更复杂的功能(简单理解为每个神经单位都是一个逻辑回归结构,都能够完成一个独立的功能)
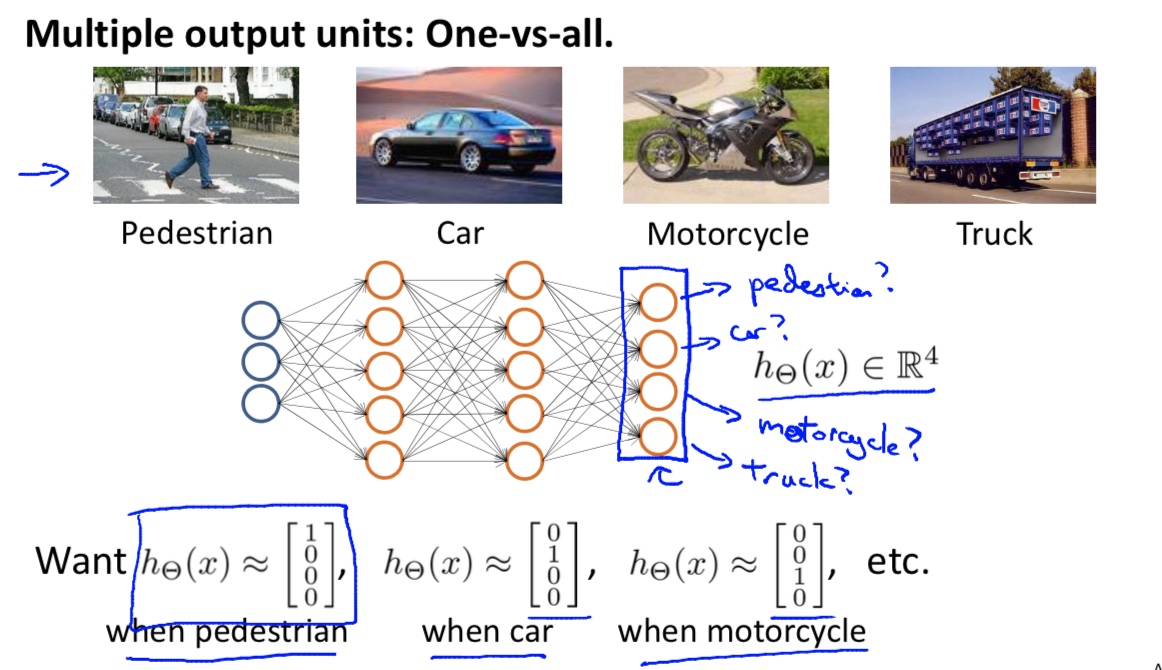
处理多分类问题
- 每个分类被一个节点判断出(像上一节类似,一个节点判断and,一个节点判断or,它们的下一层节点就能判断更复杂的内容)
- 多个分类,可以在一个神经网络中判断输出
- 逻辑回归时候,是把多分类问题,视为多个二分类问题处理的(多个$h_\theta^i(x)$)
Cost function
- 和逻辑回归的cost function非常类似,其中m表示样本数,K表示神经网络最终输出的个数,正则化项包含了所有参数
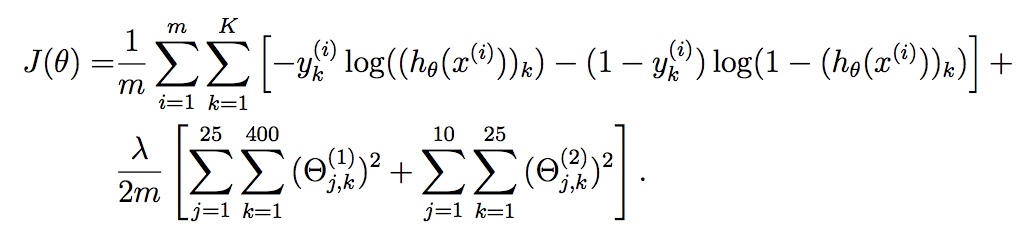
求最优解
- 求解算法最常用的当然也是使用的梯度下降,然后也可以使用深度学习中的动态梯度下降,RMProp,Adam等
- 梯度的计算也可以使用最原始的方法,对每个参数求解梯度,但是由于神经网络中参数太多,原始方法效率太低,所以有了后面的Backpropagation算法