目的
- BP 算法的目的在于为优化函数(比如梯度下降、其它的高级优化方法)提供梯度值,即使用 BP 算法计算代价函数(cost function)对每个参数的偏导值,其数学形式为:$\frac{\partial}{\partial\theta^l_{ij}}J(\theta)$,并最终得到的值存放在矩阵$\Delta^{(l)}$中。
网络结构
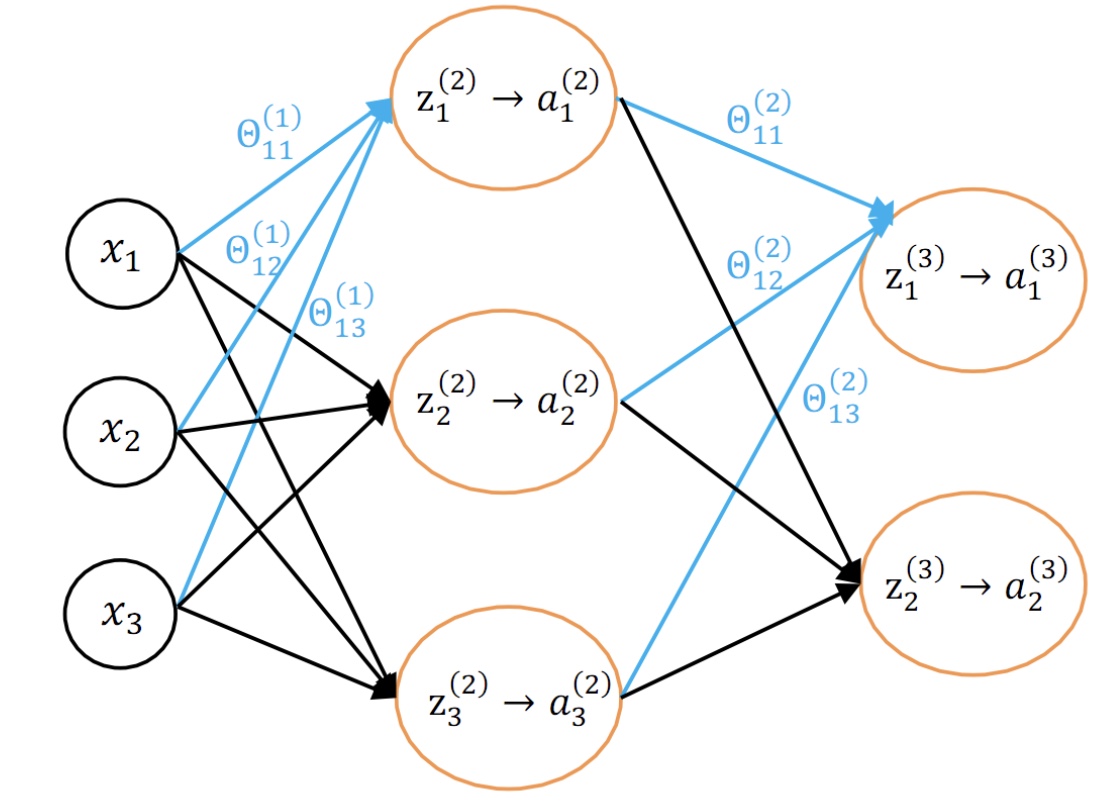
- 简单神经网络结构:
- 单个数据的代价函数:

神经网络学习算法图概览
清楚一个函数的求导对象:输入值
给定一个函数 f(x),它的首要求导对象是什么?就是它的输入值,是自变量 x。那 f(g(x)) 呢?即把g(x) 当作一个整体作为它的输入值,它的自变量。那么 g(x) 这个整体就是它的首要求导对象。因此,一个函数的求导对象是它的输入值,是它的自变量。弄清楚这一点,才能在求多元函数偏导的链式法则中游刃有余。神经网络中各数据之间的关系——谁是谁的输入值
图 3.1 自下而上,每一个框是上面一个框的输入值,也即上面一个框中函数的自变量。这张图明确了神经网络中各数据之间的关系——谁是谁的输入值,图中表现得非常清楚。上段提到一个函数的求导对象是它的输入值,那么通过图 3.1 就能非常方便地使用链式法则,也能清楚地观察到 BP 算法的流程(后面一个小节会给出一个更具体的 BP 流程图)。神经网络的学习(训练)流程(前馈传播和BP算法)
对照文首给出的图 1.1 神经网络的模型图,应该很容易理解图 3.1 的含义,它大致地展现了神经网络的学习(训练)流程。前馈传播算法自下而上地向上计算,最终可以得到 a(3),进一步可以计算得到 J(Θ)。而 BP 算法自顶向下,层层求偏导,最终得到了每个参数的梯度值。下面一个小节将仔细介绍本文的主题,即 BP 算法的流程图解。

BP 算法的直观图解
- BP 算法的流程在这张图中清晰可见:自顶向下(对应神经网络模型为自输出层向输入层)层层求偏导(核心:找准谁是谁的输入,对求偏导尤其重要)
- 所以 BP 算法即反向传播算法,就是自顶向下求代价函数$J(\theta)$ 对各个参数$\theta^l_{ij}$ 偏导($\frac{\partial}{\partial\theta^l_{ij}}J(\theta)$)的过程,对应到神经网络模型中即自输出层向输入层层层求偏导
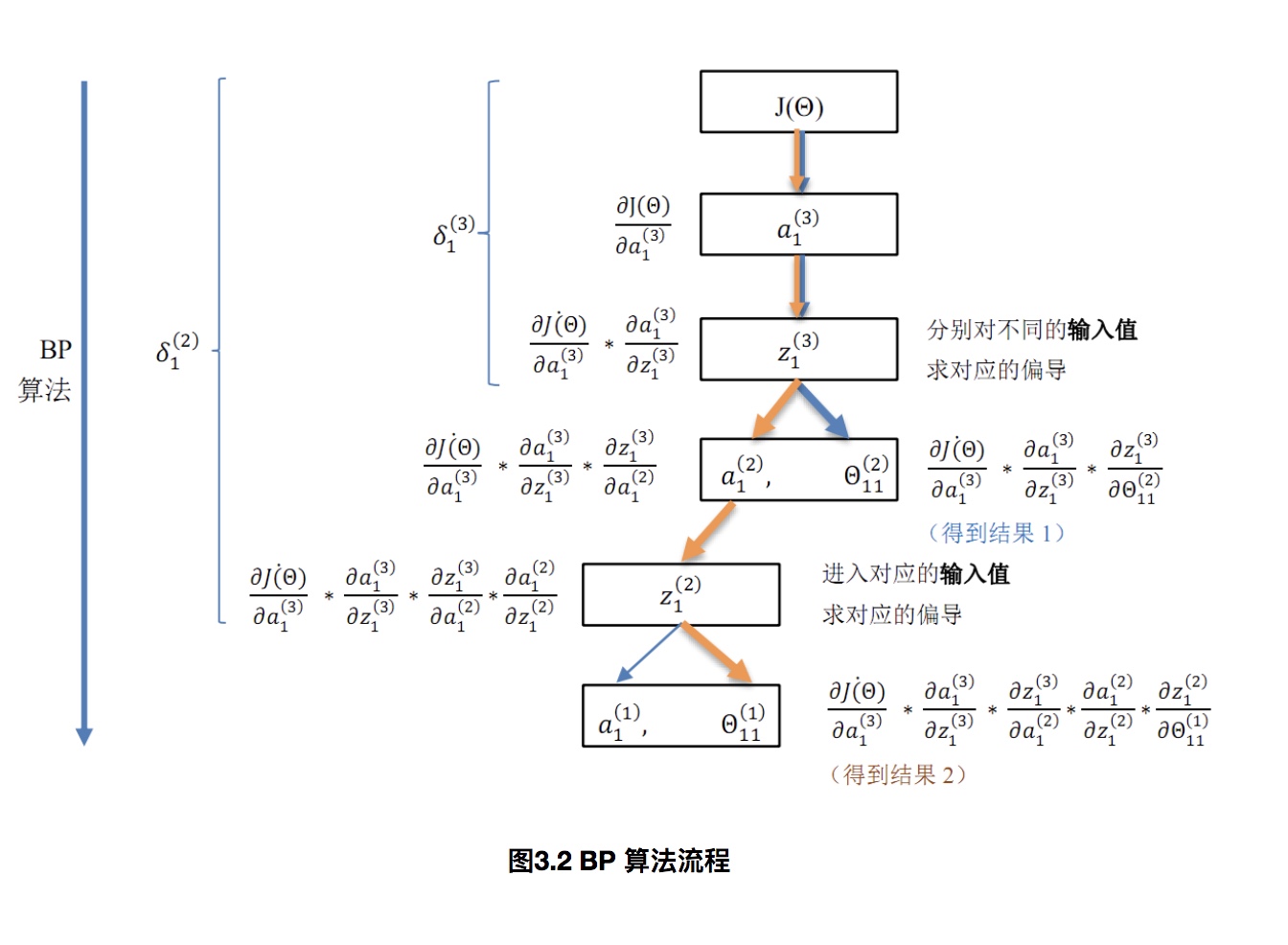
从这里可以看出:,为什么要使用BP算法:
- 自输出层向输入层(即反向传播),逐层求偏导,在这个过程中逐渐得到各个层的参数梯度。
- 在反向传播过程中,使用$\delta(l)$ 保存了部分结果,从而避免了大量的重复运算。
详细推导计算过程可以参考原文