参考文章:
机器之心:读懂概率图
图模型
- 图模型为很多存在依赖关系的真实世界任务提供了可以解释的建模方式。图模型为我们提供了一种用有原则的方式解决这些任务的方法
- 概率图模型(PGM/probabilistic graphical model)是一种用于学习这些带有依赖(dependency)的模型的强大框架
图的每个节点(node)都关联了一个随机变量,而图的边(edge)则被用于编码这些随机变量之间的关系
- 我们可以将图的模式分为两大类——贝叶斯网络(Bayesian network)和马尔可夫网络(Markov networks)
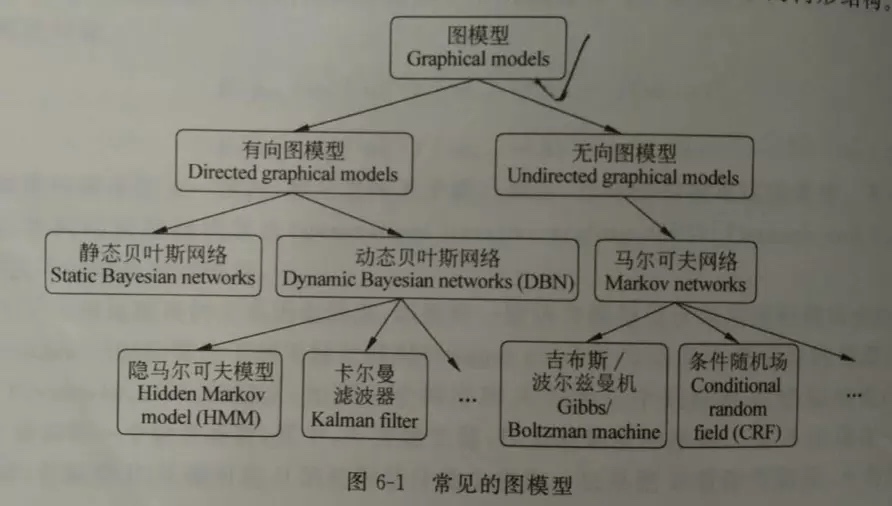
- 我们可以将图的模式分为两大类——贝叶斯网络(Bayesian network)和马尔可夫网络(Markov networks)
“生成式”(generative)模型考虑联合分布P(Y,R,O);
“判别式”(discriminative)模型考虑条件分布P(Y,R|O);条件独立
- 图结构实际上带有关于这些变量的重要信息。具体来说,它们定义了这些变量之间的一组条件独立(conditional independence),也就是这种形式的陈述——「如果观察到 A,那么 B 独立于 C。」
有向图模型:贝叶斯网络
“生成式”(generative)模型考虑联合分布P(Y,R,O),属于生成模型,借助有向无环图(DAG图)来刻画属性简的依赖关系,并使用条件概率表来描述属性的联合概率分布,这里重点是计算联合概率分布
- 例子
- 让我们看看与每个节点关联的表格,它们的正式名称是条件概率分布(CPD/conditional probability distribution)
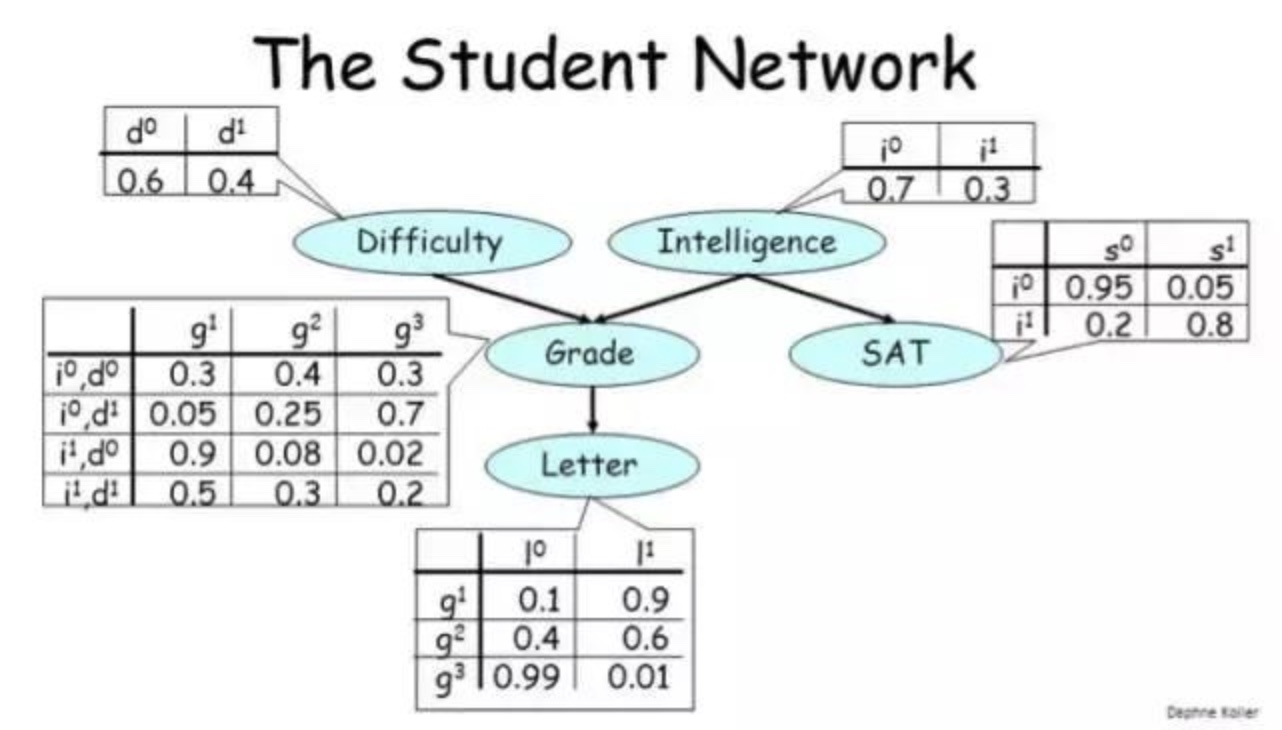
- 让我们看看与每个节点关联的表格,它们的正式名称是条件概率分布(CPD/conditional probability distribution)
隐马可科夫模型
隐马尔可夫模型(Hidden Markov Model,简称HMM)是结构最简单的动态贝叶斯网(dynamic Bayesian network),这是一种著名的有向图模型,主要用于时序数据建模,在语音识别、自然语言处理等领域有广泛应用
其中几个重要的参数:
- a.状态转移概率,y1,y2….的转移概率。
- b.输出观察概率y输出x的概率。
- c.初始状态概率,y1
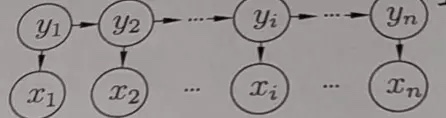
HMM解决的问题
- 如何评估模型与观测序列之间的匹配程度,例如许多任务已有观察序列{x1,x2,x3…xn-1}求x(n)的最有可能值,就是转换为判定模型,$P(x|\theta)$最大的匹配程度
- 根据观测序列推断出隐藏的模型状态,已经{x1,x2,x3…x(n)},求{y1,y2,y3…y(n)}。如语音识别中,观测值为语音符号,隐藏状态为文字
- 如何训练模型,使其能最好的描述观测数据,即调整模型参数[A,B,PI],使得该观测序列出现的概率最大
马尔可夫随机场
马尔科夫随机场是典型的马尔科夫网络,是一种著名的无向图模型,多个变量之间的联合概率分布能够基于团分解为多个因子的乘积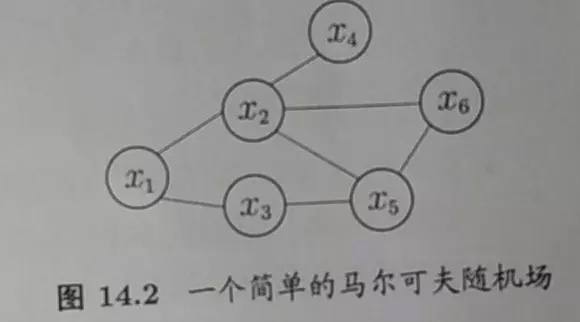
团:
对于图中的任意两点都有线相连,则称该结点子集为一个”团”,若在一个团中加入另外的节点都不再形成团,那么陈该该结点子集为”极大团”势函数:
亦称”因子”(factor),这是定义在变量子集上的非负实函数,主要用于定义概率分布函数:多个变量之间的联合概率分布能够基于团分解为多个因子的乘积
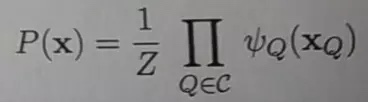
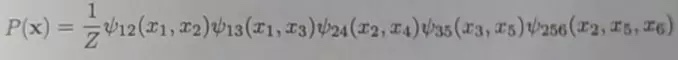
条件随机场
是一种判别式无向图模型,对条件分布进行建模。试图对多个变量在给定观测值后的条件概率进行建模。
- 具体说就是给定$X={x_1,x_2,x_3,….x_n}和Y={y_1,y_2,y_3…y_n}$然后建立模型P(Y|X)。然后对后面给定的$(x_{11},x_{12},x….)$直接使用P(Y|X)模型进行预测。标记变量y可以是结构型变量,即其分量直接具有某种相关性
学习和推断
学习(参数估计):
如果都知道各个变量,各个属性间的依赖关系,只需要对各个条件概率表进行计数,就能够得到联合概率分布。但实际情况中几乎不会轻易得到所有的关系依赖,所有贝叶斯网络的首要任务是根据训练数据找出最“恰当”的贝叶斯网,也就是学习出属性间的依赖关系,得到联合概率分布。使用的是评分函数算法推断(推理):通过第一步的学习得到了联合概率分布,属性,变量间的依赖关系,也就是得到了贝叶斯网络后,就可以通过它来回答”查询”,及通过一些已知属性变量的观测值来预测一些其他的属性
我们可以使用推理来解答一些问题:
- 边际推理(marginal inference):寻找一个特定变量的概率分布。比如,给定一个带有变量 A、B、C 和 D 的图,其中 A 取值 1、2 和 3,求 p(A=1)、p(A=2) 和 p(A=3)。
- 后验推理(posterior inference):给定某些显变量 v_E(E 表示证据(evidence)),其取值为 e,求某些隐藏变量 v_H 的后验分布 p(v_H|v_E=e)。
- 最大后验(MAP)推理(maximum-a-posteriori inference):给定某些显变量 v_E,其取值为 e,求使其它变量 v_H 有最高概率的配置
解答这些问题的流行的算法
其中既有精准的算法,也有近似的算法。所有这些算法都既可用于贝叶斯网络,也可用于马尔可夫网络- 精确推断方法
希望能计算出目标变量的边际分布或条件分布的精确值。遗憾的是,一般情形下,此类算法的计算复杂度随着极大团规模的增长呈指数增长,适用范围有限- 变量消去
精确推断的实质是一类动态规划算法,它利用图模型所描述的条件独立性来消减计算目标概率值所需的计算量。变量消去是最直观的精确推断算法,也是构建其他精确推断算法的基础。
变量消去法有一个明显的缺陷:若需计算多个边际分布,重复使用变量消去法将对造成大量的冗余计算。 - 信念传播
信念传播(Belief Propagation)算法将变量消去法中的求和操作看作一个消息传递过程,较好的解决了求解多个边际分布时重复计算问题。
- 变量消去
- 近似推断方法
希望在较低时间复杂度下获得原问题的近似解。此类方法在现实任务中更常用- 采样:通过使用随机化方法完成近似
- MCMC采样:概率图模型中最常用的采用技术是马尔可夫链蒙特卡罗(Markov Chain Monte Carlo,简称MCMC)方法
- 变分推断(variational inference)
- 变分推断通过使用已知简单分布来逼近所需推断的复杂分布,并通过限制近似分布的类型,从而得到一种局部最优、但具有确定解的近似后验分布
- 采样:通过使用随机化方法完成近似
- 精确推断方法
应用举例
三门问题(贝叶斯网络)
- 问题描述:
主持人会向你展示三扇关着的门,其中一扇门之后有一辆车,其它门后则有一些无价值的东西。你可以选择一扇门。然后,主持人会打开剩下的两扇门中没有车的一扇。现在,你可以选择是否更换选择的门:坚持你之前选择的那扇门,还是选择主持人剩下的那扇关闭的门。你会更换吗?- 直觉上看,主持人似乎并没有透露任何信息。事实证明这种直觉并不完全正确。让我们使用我们的新工具「图模型」来理解这个问题

- 直觉上看,主持人似乎并没有透露任何信息。事实证明这种直觉并不完全正确。让我们使用我们的新工具「图模型」来理解这个问题
- 网络构造
- 定义变量
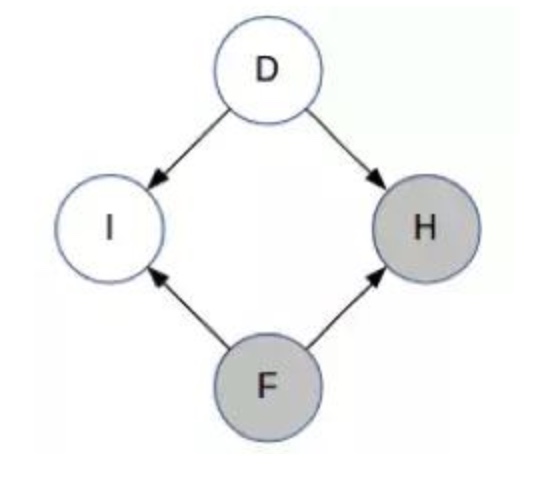
- D:背后有车的门
- F:你的第一个选择
- H:主持人打开的门
- I:F 是否是 D?
- D、F 和 H 可取值为 1、2 或 3;I 可取值 0 或 1。D 和 I 是未被观察到的,而 F 是已观察到的。在主持人打开其中一扇门之前,H 都是未被观察到的。因此,我们使用贝叶斯网络来解决我们的问题
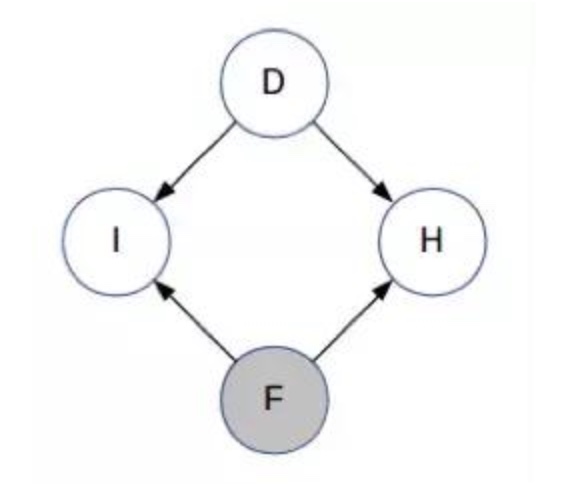
- 定义变量
- 计算逻辑
注意箭头的方向——D 和 F 是相互独立的,I 显然依赖于 D 和 F,主持人选择的门也取决于 D 和 F。目前你对 D 还一无所知。(这与学生网络的结构类似,即知道学生的智力水平不能让你获得有关课程难度的任何信息- 现在,主持人选择了门 H 并打开了它。所以现在 H 已被观察到
- 然后下面就是通过计算变量的CPD来得到最大的条件概率(判别式模型),详情见机器之心:读懂概率图
- 现在,主持人选择了门 H 并打开了它。所以现在 H 已被观察到
- 问题描述:
图像去噪
真实图像和噪音图像


目标:现在你的目标是恢复原始图像。让我们看看如何使用概率图模型来实现
思考步骤
- 首先第一步是思考哪些变量是观察得到的,哪些变量不能观察到,以及我们可以如何将它们连接起来构成一个图
- 让我们将有噪声图像中的每个像素都定义为一个观察到的随机变量,并将基准图像中的每个像素都定义为一个未被观察到的变量。由此,如果该图像的大小为 MxN,那么观察到的变量和未被观察到的变量都各有 MN 个。让我们将观察到的变量表示为 X_ij,未被观察到的变量定义为 Y_ij。每个变量都可取值 +1 或 -1(分别对应于黑色像素和白色像素)。
- 模型:给定观察到的变量,我们希望找到未观察到的变量的最有可能的值。这对应于 MAP 推理
现在让我们使用一些领域知识来构建图结构。很显然,在有噪声图像中的 (i,j) 位置观察到的变量取决于在基准图像中的 (i,j) 位置未观察到的变量。原因是大多数时候它们是相等的。
我们还能得到什么信息?对于基准图像,邻近的像素通常有一样的值——在颜色变化的边界不是这样,但在每个单一颜色的区域内有这个性质。因此,如果 Y_ij 和 Y_kl 是邻近像素,那么我们将它们连接起来
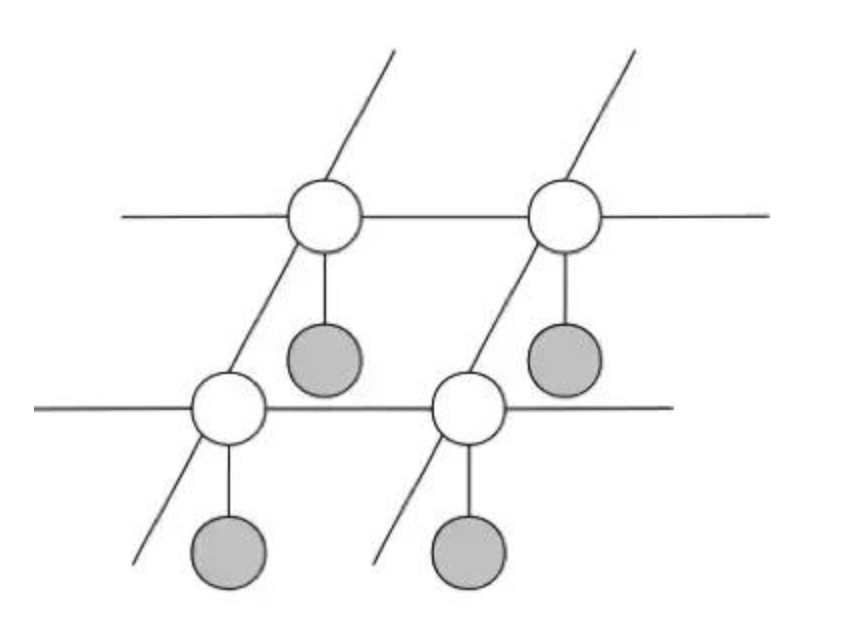
图结构
- 其中,白色节点表示未被观察到的变量 Y_ij,灰色节点表示观察到的变量 X_ij。每个 X_ij 都连接到对应的 Y_ij,每个 Y_ij 都连接到它的相邻节点。
- 注意这是一个马尔可夫网络,因为图像的像素之间不存在因果关系,因此这里不适合使用贝叶斯网络中有方向的箭头