习题代码:Face-Recognition and Neural-Style-Transfer
人脸识别(Siamese网络)
一般分为验证和识别两步

One-shot learning
- 背景:人脸识别的train是很少的图片,并且一般只给你一张图片你就得识别出来,并不是想普通的图片识别一样,有很多的样本。比如新加入的新同事,之前并没有样本
- 方法:和图片库已有的少量图片做相似度比较

- 如何实现:可以使用Siamese network
Siamese network
- 将图片映射为n维向量,将$f(x^{(1)})$看做是$x^{(a)}$的编码,然后通过比较不同图片的编码的差别来区分是否是同一个人
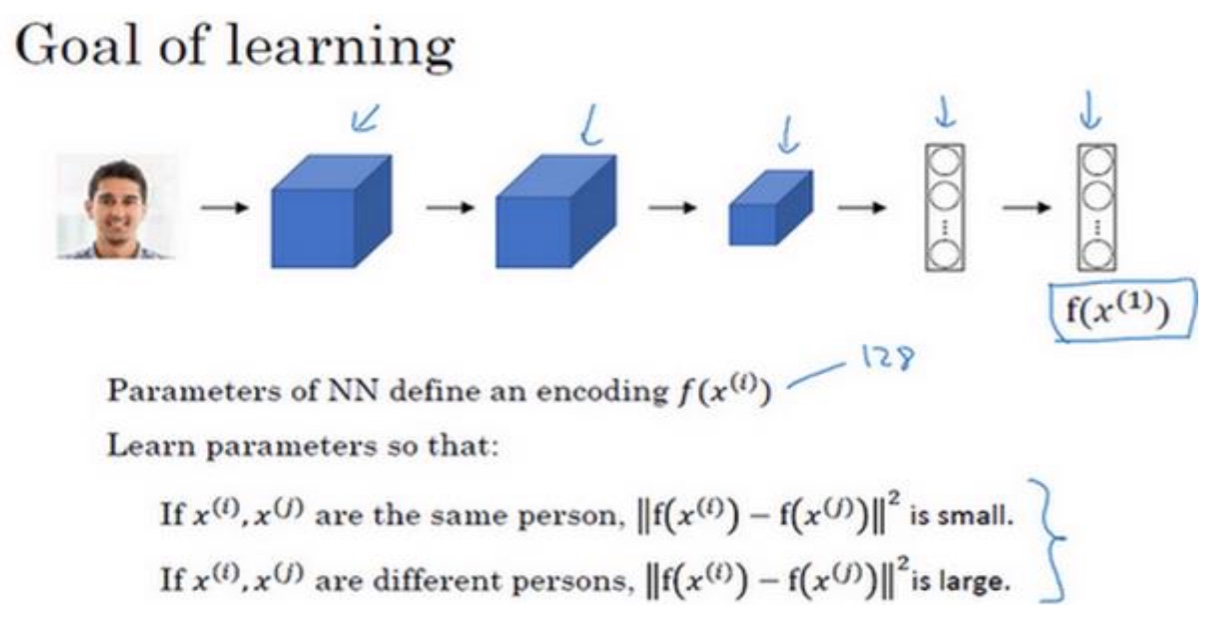
- 那么怎么判断输出的图片编码好与差呢?可以使用下面的三元组(Triplet)损失函数达到目的
- 将图片映射为n维向量,将$f(x^{(1)})$看做是$x^{(a)}$的编码,然后通过比较不同图片的编码的差别来区分是否是同一个人
Triplet损失
- 定义:需要Anchor图片,Postive图片,Negative图片,简写为A,P,N
- 避免网络输出无用,有一个$\alpha$超参数,控制A,P和A,N之间的差距
$||f(A)-f(P)||^2 - ||f(A)-f(N)||^2 + \alpha <= 0$ - Loss function
如果目标已经ok,那么值为0,可以看见各种场景只需要找到合适的损失函数,然后下面的步骤都类似(用梯度下降等方法求出极值)
L(A,P,N)=max($||f(A)-f(P)||^2 - ||f(A)-f(N)||^2 + \alpha$, 0) - 训练数据需要注意的地方
- 需要注意训练集的对一个人需要多张照片,至少要满足Anchor,Posistion
- 尽量选择d(A,P)$\approx$d(A,N),这样能够学习到更多内容,如果差别太大,很容易判断,不能学习到有效数据
- 算法步骤:
- 目的,学习到一种好的编码映射f(x)
- 1.定义好A,P,N数据集
- 2.用梯度下降最小化我们之前定义的代价函数J
- 这样做的效果就是用反向传播来学习到一种编码方式,如果是同一个人,那么d就很小,如果是不同的人,那么d就会很大
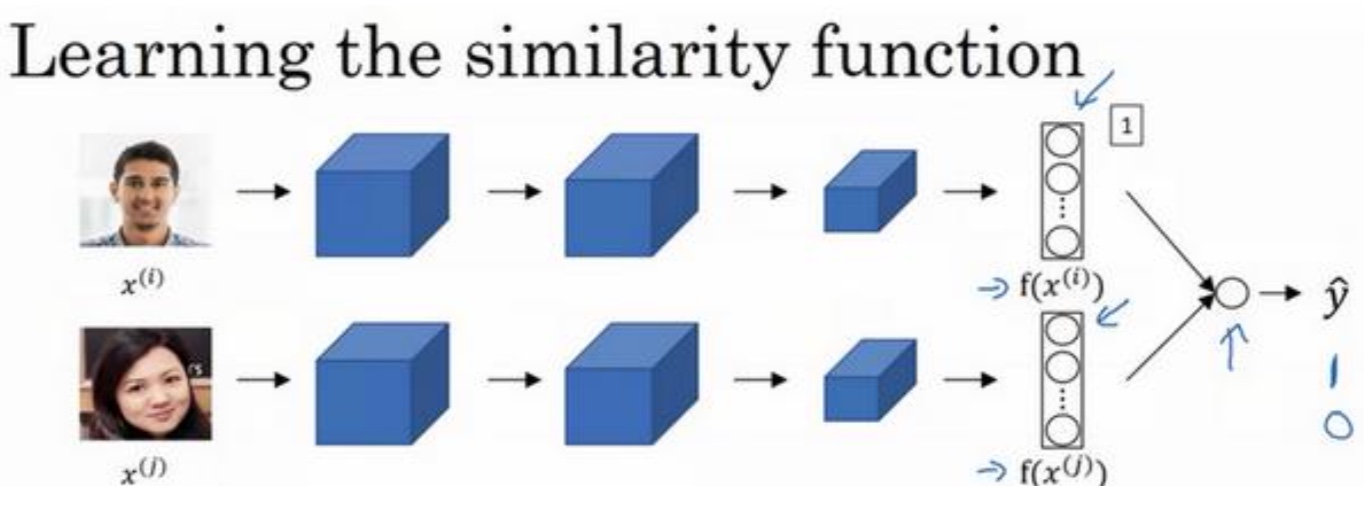
面部识别与二分类(Siamese变种)
- 原始Siamese网络是直接计算编码的L2距离,这里可以将编码经过激活函数,比如sigmoid的处理,来实现分类的目的
- $\hat y = sigmoid(\sum_{(k=1)}^{128}w_i|f(x^{(i)})_k - f(x^{(j)})_k|+b)$,当然$|f(x^{(i)})_k - f(x^{(j)})_k|$这一部分还可以替换为其他的相似度计算方法,比如$\chi$平方相似度
- 还注意下它的输入为成对图片的输入,比如两张同一个人的照片,输出为1。两种不同人的照片,输出就为0
神经风格转换
- 什么是神经风格转换

- 什么是深度卷积网络(需要直观感受到不同层次的网络提取的特征,深层和前层是如何计算的)
- 相关概念
- 一个神经元就表示一个filter的及输出,在输出中就表示一个通道,也代表一个特征,经常会有多个通道,就是多种filter,代表不同的特征
- 神经单元激活最大化,比如激活函数是sigmoid,我理解只有在边界两端的值,才能有更明确的分类结果,相应的特征表现也最好
- 各层的特征
- 第一层:主要表现对一些线条,边缘或者特点的颜色等低维特征比较感兴趣
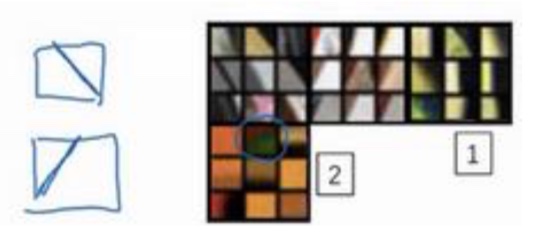
- 第二层:通常能够看到图片更大的区域,能够检测到更复杂的模型

- 后面的第三层,第四层….等就能够检测到更具体的事物了


- 第一层:主要表现对一些线条,边缘或者特点的颜色等低维特征比较感兴趣
- 相关概念
神经风格迁移系统的(Cost function)
要构造一个神经风格迁移系统,我们需要给生成的图像定义一个代价函数
- J(G)=$\alpha J_{content}(C,G) + \beta J_{stype}(S,G)$
- 内容代价函数:就是计算原始图片和生成图片的某一层的激活值的相似度
- 选取一个预训练模型,比如是VGG卷积模型
- 选取中间层l,一般不会太深,也不好太浅
- 计算一对一对的训练数据(一张原始图片,一张生成图片),分别计算在l层的激活值,然后对比他们的相似度(可以用L2范数)
- $J_{content}(C,G)=\frac{1}{2}||a^{[l][C]}-a^{[l][G]}||^2$
- 下面是风格代价函数的介绍
- What you should remember:
- Neural Style Transfer is an algorithm that given a content image C and a style image S can generate an artistic image
- It uses representations (hidden layer activations) based on a pretrained ConvNet.
- The content cost function is computed using one hidden layer’s activations.
- The style cost function for one layer is computed using the Gram matrix of that layer’s activations. The overall style cost function is obtained using several hidden layers.
- Optimizing the total cost function results in synthesizing new images.
风格代价函数(style cost function)
- 定义:现在你选择了某一层𝑙,比如这一层去为图片的风格定义一个 深度测量,现在我们要做的就是将图片的风格定义为𝑙层中各个通道之间激活项的相关系数
- 理解CNN中的神经元
- 一个神经元就表示一个filter的及输出,在输出中就表示一个通道,也代表一个特征
- 这个红色的通道(编号1)对应(编号 3),它能找出图片中的特定位置是否含有这些垂直的纹理
- 而第二 个通道也就是黄色的通道(编号 2),对应这个神经元(编号 4)

- 一个神经元就表示一个filter的及输出,在输出中就表示一个通道,也代表一个特征
- 理解相关系数
- 定义:相关系数这个概念为你提供了一种去测量这些不同的特征的方法,比如这些垂直纹理,这些橙色或是其他的特征去测量它们在图片中的各个位置同时出现或不同时出现的频率
- 意义:通过测量,你能得知在生成的
图像中垂直纹理和橙色同时出现或者不同时出现的频率,这样你将能够测量生成的图像的风格与输入的风格图像的相似程度
- 风格矩阵(Gram matrix)(Correlation between filters):
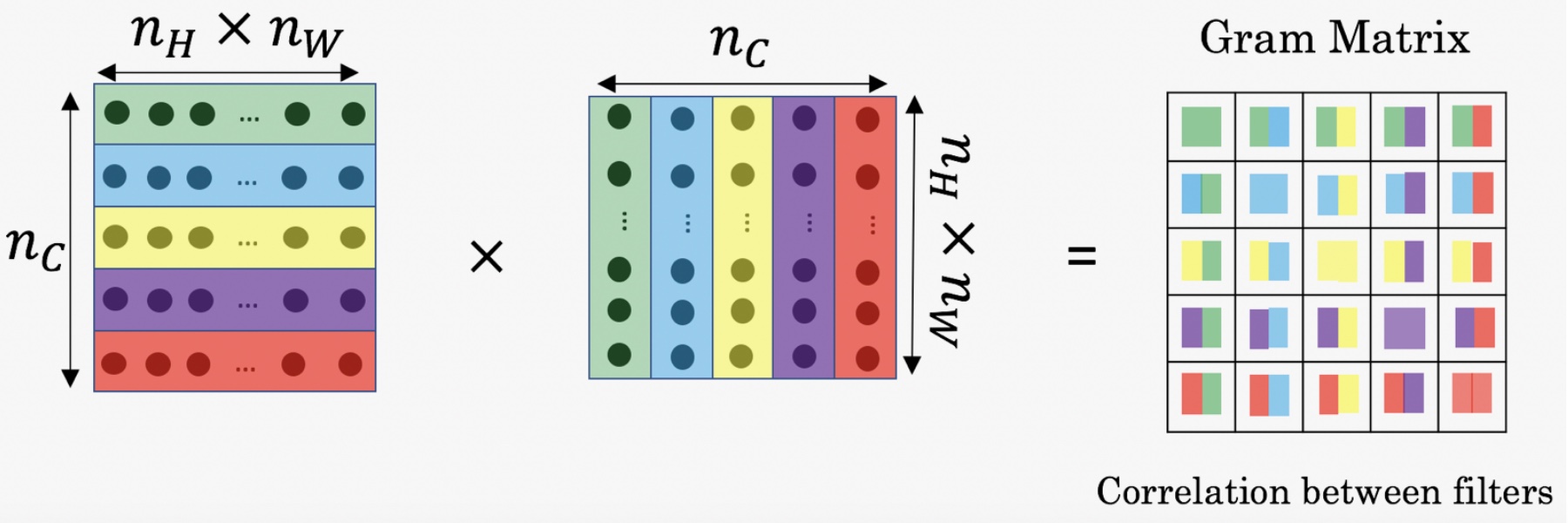
- 通过对k和k’通道中中所有的数值(注意是激活值,不是各个filter的值)进行计算就得到了𝐺矩阵,也就是风格矩阵
- 如果不相关,那么$G^{[l]}_{KK’}$会比较小,否则就会很大
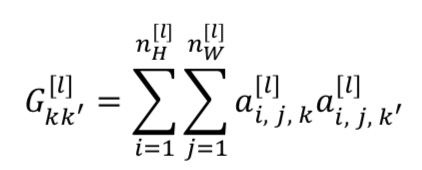
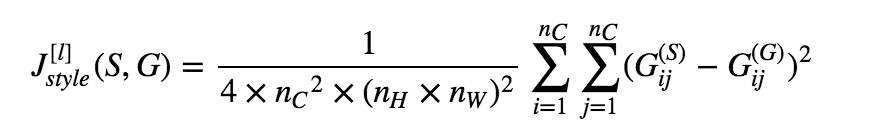 code:
code:
- 分别计算出G和S图片的矩阵,然后带入下面的cost function这将得到这两个矩阵之间的误差
- Cost function
- 直观感受:就是对两张图片分别计算不同通道的输出的相关性G1,G2(上面的风格矩阵)(Gram matrix就展示的不同激活值(filter输出)之间相似度,有点像协方差),然后再优化使这两张图片的不同通道的值差距减小,即类似于$\sum(G1-G2)$,cost越小,表示两越相近
- 一般只计算其中一层的cost,当然可以对每层都这样计算cost,然后相加,但要复杂一些

- 这是两个矩阵间一个基 本的 Frobenius 范数

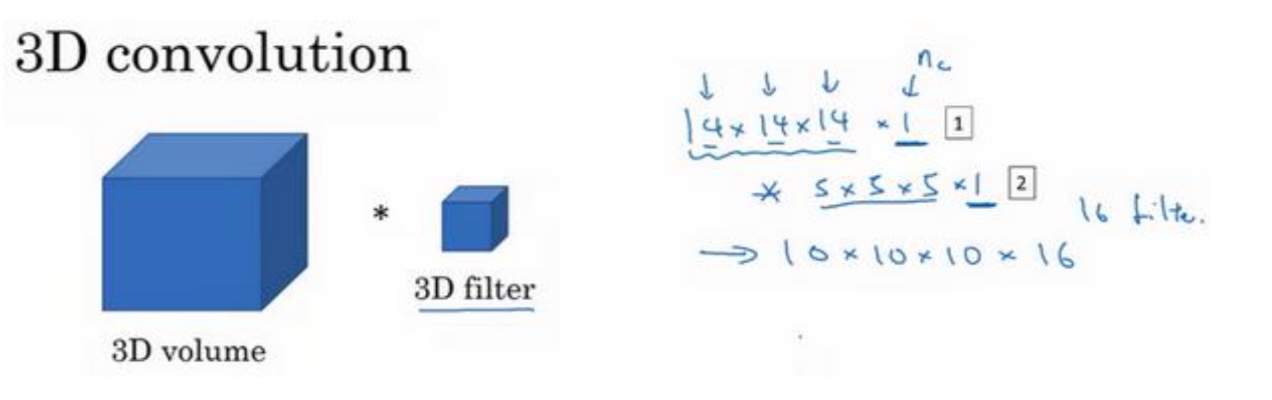
CNN同样适合于一维到三维
CNN同样适合于一维和三维数据,但对一维数据(和时间序列相关的)的处理,更常见的使用RNN
- 一维
比如心电图信息处理等,它的卷积核更像是一维的滑动窗口一样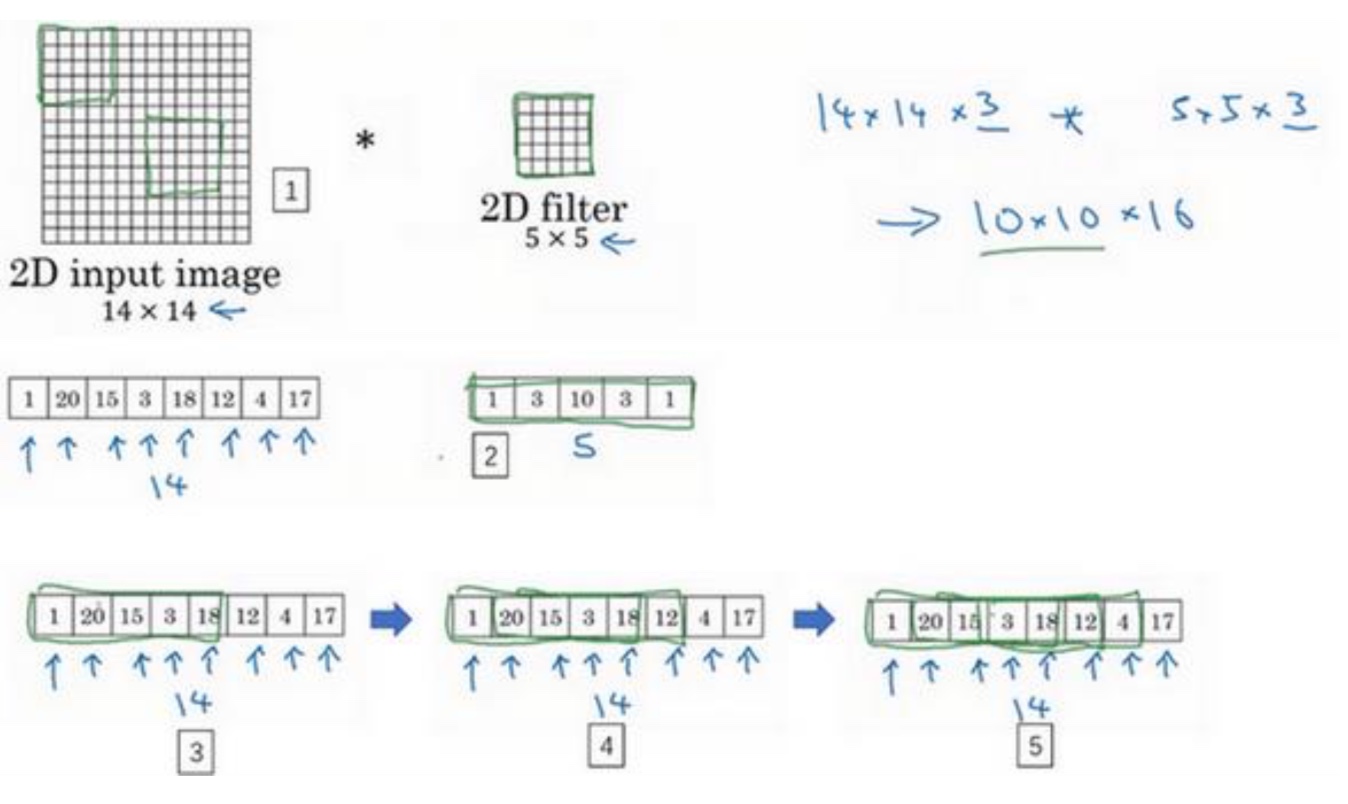
- 三维
比如在CT图像上,一张图片就是人体的一个切面,当然这种情况它的卷积核也是三维的,并且也可以有通道数