背景
- 求解强化学习问题可以理解为如何最大化个体在与环境交互过程中获得的累积奖励
- 当环境状态是完全可观测时,个体可以通过构建马尔科夫决策过程来描述整 个强化学习问题。有时候环境状态并不是完全可观测的,此时个体可以结合自身对于环境的历史 观测数据来构建一个近似的完全可观测环境的描述
- 从这个角度来说,几乎所有的强化学习问题 都可以被认为或可以被转化为马尔科夫决策过程
马尔科夫过程
马尔科夫性
在一个时序过程中,如果 t + 1 时刻的状态仅取决于 t 时刻的状态 $S_t$ 而与 t 时刻之前的任 何状态都无关时,则认为 t 时刻的状态$S_t$ 具有马尔科夫性 (Markov property)
马尔科夫过程(马尔科夫链)
若过程中的每一 个状态都具有马尔科夫性,则这个过程具备马尔科夫性。具备了马尔科夫性的随机过程称为马尔 科夫过程 (Markov process),又称马尔科夫链 (Markov chain)
- 描述一个马尔科夫过程的核心是状态转移概率矩阵
$P_{ss′} = P [S_{t+1} = s′|S_t = s]$ - 通常使用一个元组 ⟨S, P ⟩ 来描述马尔科夫过程,其中 S 是有限数量的状态集,P 是状态转 移概率矩阵
采样
从符合马尔科夫过程给定的状态转移概率矩阵生成一个状态序列的过程称为采样(sample)。
状态序列
采样将得到一系列的状态转换过程,本书我们称为状态序列 (episode)
完整状态序列
当状态序列的最后一个,状态是终止状态时,该状态序列称为完整的状态序列 (complete episode)
马尔科夫奖励过程
背景
马尔科夫过程只涉及到状态之间的转移概率,并未触及强化学习问题中伴随着状态转换的 奖励反馈。如果把奖励考虑进马尔科夫过程,则成为马尔科夫奖励过程(Markov reward process, MRP)。它是由 ⟨S, P, R, γ⟩ 构成的一个元组,其中:
- S 是一个有限状态集
- P 是集合中状态转移概率矩阵:$P_{ss′} = P [S_{t+1} = s′|S_t = s]]$
- R 是一个奖励函数:$R_s = E [R_{t+1}|S_t = s]$
- γ 是一个衰减因子:γ ∈ [0, 1]
相关概念
- 收获
收获(return)是一个马尔科夫奖励过程中从某一个状态 $S_t$ 开始采样直到终止状态时所有 奖励的有衰减的之和。数学表达式如下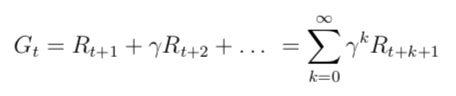
- 价值
价值(value) 是马尔科夫奖励过程中状态收获的期望。ta 数学表达式为
$v(s) = E [G_t|S_t = s]$ 价值函数
如果存在一个函数,给定一个状态能得到该状态对应的价值,那么该函数就被称为价值函数 (value function)。价值函数建立了从状态到价值的映射
马尔科夫奖励过程中的贝尔曼方程
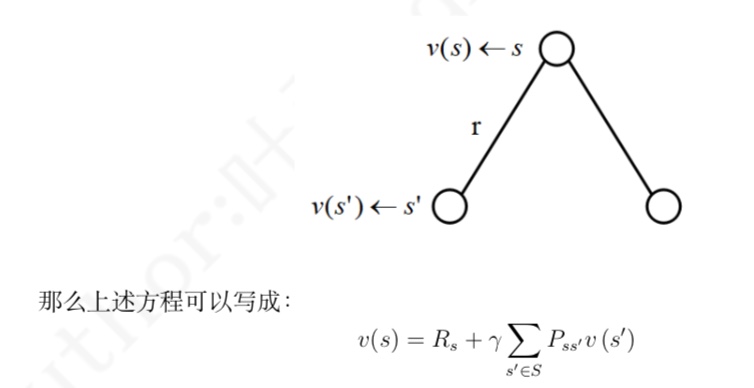
- 它(上图)提示一个状态的价值 由该状态的奖励以及后续状态价值按概率分布求和按一定的衰减比例联合组成
- 根据马尔科夫奖励过程的定义,$R_{t+1}$ 的期望就是其自身,因为每次离开同一个状 态得到的奖励都是一个固定的值。而下一时刻状态价值的期望,可以根据下一时刻状态的概率分 布得到。如果用 s′ 表示 s 状态下一时刻任一可能的状态:
马尔科夫决策过程(MDP)
背景
马尔科夫奖励过程并不能直接用来指导解决强化学习问题,因为它不涉及到个体行为的选 择,因此有必要引入马尔科夫决策过程。马尔科夫决策过程(Markov decision process, MDP)是 由 ⟨S, A, P, R, γ⟩ 构成的一个元组,其中:
- S 是一个有限状态集
- A 是一个有限行为集
- P 是集合中基于行为的状态转移概率矩阵:$P^a_{ss’} = E [R_{t+1} |S_t = s, A_t = a]$
- R 是基于状态和行为的奖励函数:$R_s^a = E [R_{t+1}|S_t = s, A_t = a]$
- γ 是一个衰减因子:γ ∈ [0, 1]
相关概念
策略
个体在给定状 态下从行为集中选择一个行为的依据则称为策略 (policy),用字母 π 表示。策略 π 是某一状态下基于行为集合的概率分布:
$π(a|s)=P[A_t =a|S_t =s]$- 策略仅通过依靠当前状态就可以产生一个个体的行为,可以说策略 仅与当前状态相关,而与历史状态无关
- 策略描述的是个体的行 为产生的机制,是不随状态变化而变化的,被认为是静态的
随机策略
随机策略是一个很常用的策略,当个体使用随机策略时,个体在某一状态下选择的行为并不 确定。借助随机策略,个体可以在同一状态下尝试不同的行为当给定一个马尔科夫决策过程:M = ⟨S, A, P, R, γ⟩ 和一个策略 π,那么状态序列 $S_1, S_2$, . . . 是一个符合马尔科夫过程 $⟨S, P_π⟩$ 的采样
价值函数
价值函数 $v_π(s)$ 是在马尔科夫决策过程下基于策略 π 的状态价值函数,表示从状态 s 开始,遵循当前策略 π 时所获得的收获的期望:$v_π(s) = E [G_t|S_t = s]$行为价值函数(状态行为对价值函数)
一个基于策略 π 的行为价值函数 $q_π(s,a)$,表示在遵循策略 π 时,对当前状态 s 执行某一具体行为 a 所能的到 的收获的期望:$q_π(s,a) = E[G_t|S_t = s,A_t = a]$- 贝尔曼方程
同理,可推导出如下两个方程
$v_π(s) = E [R_{t+1} + γv_π(S_{t+1})|S_t = s]$
$q_π(s, a) = E [R_{t+1} + γq_π(S_{t+1}, A_{t+1})|S_t = s, A_t = a]$
状态价值和行为价值转换
一个状态的价值可以用该状态下所有行为价值来表达:
$v_\pi(s) = \sum \pi(a|s)q_\pi(s,a) (a\in A)$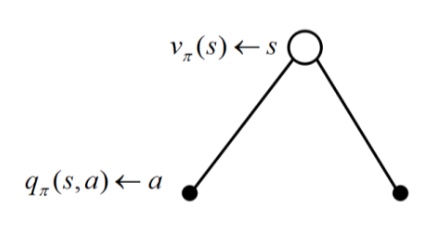
一个行为的价值可以用该行为所能到达的后续状态的价值来表达:
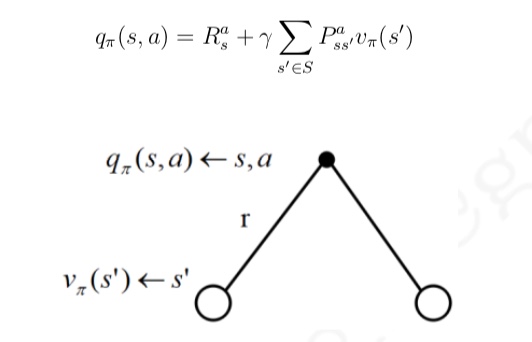
把上二式组合起来,可以得到下面的结果:
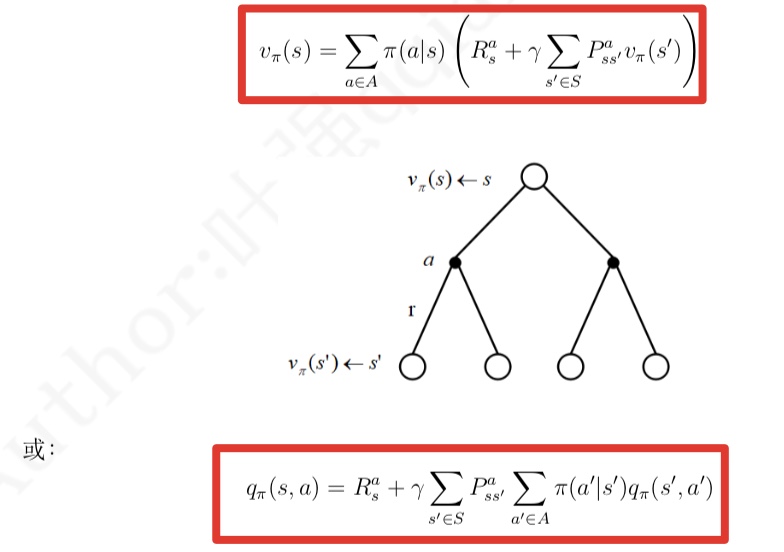
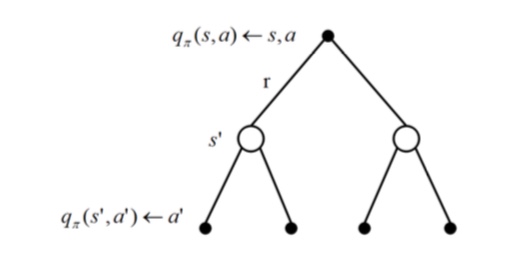
最优价值函数
- 背景:
是否存在一个基于某一策略的价值函数, 在该策略下每一个状态的价值都比其它策略下该状态的价值高?如果存在如何找到这样的价值 函数?这样的价值函数对应的策略又是什么策略? - 最优状态价值函数
是所有策略下产生的众多状态价值函数 中的最大者:$v_∗ = max (v_π(s))$ - 最优行为价值函数(optimal action-value function)
是所有策略下产生的众多行为价 值函数中的最大者:$q_∗(s,a) = max q_π(s,a)$ - 贝尔曼优化方程
- 最优状态行为价值
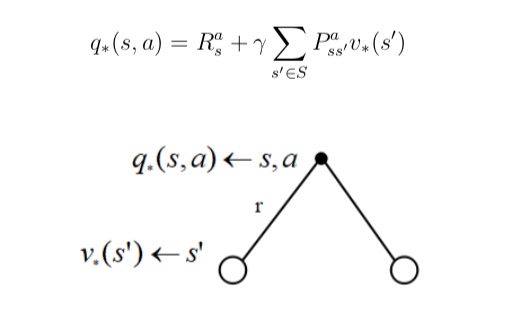
- 也可以由后续状态行为价值函数得到
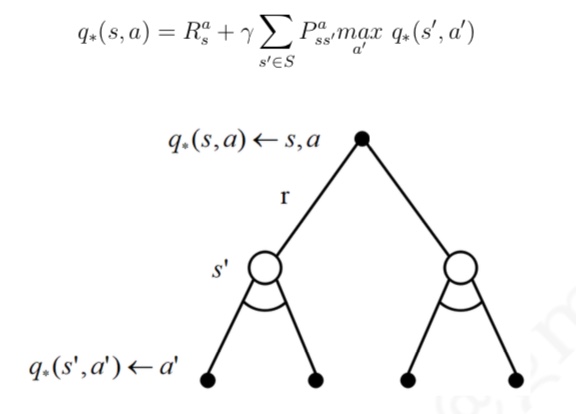
- 也可以由后续状态行为价值函数得到
- 最优状态价值:
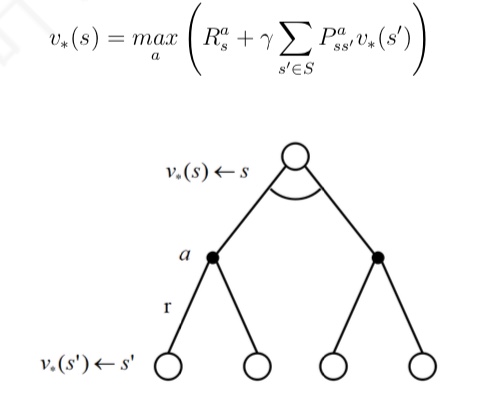
- 最优状态行为价值