动态规划寻找最优策略

发表于 | 分类于 ，

背景

动态规划理解

  • 规划
    “规划”是在已知环 境动力学的基础上进行评估和控制，具体来说就是在了解包括状态和行为空间、转移概率矩阵、 奖励等信息的基础上判断一个给定策略的价值函数，或判断一个策略的优劣并最终找到最优的 策略和最优价值函数

  • 动态规划算法把求解复杂问题分解为求解子问题，通过求解子问题进而得到整个问题的解,在解决子问题的时候，其结果通常需要存储起来被用来解决后续复杂问题

    • 当问题具有下列两个 性质时，通常可以考虑使用动态规划来求解:
      • 第一个性质是一个复杂问题的最优解由数个小问题 的最优解构成，可以通过寻找子问题的最优解来得到复杂问题的最优解;
      • 第二个性质是子问题在 复杂问题内重复出现，使得子问题的解可以被存储起来重复利用

  • 和马尔科夫决策过程关系
    马尔科夫决策过程具有上述两 个属性:

    • 贝尔曼方程把问题递归为求解子问题
    • 价值函数相当于存储了一些子问题的解，可以复 用。因此可以使用动态规划来求解马尔科夫决策过程

预测和控制

  • 预测 (prediction):已知一个马尔科夫决策过程 MDP ⟨S, A, P, R, γ⟩ 和一个策略 π，或者是 给定一个马尔科夫奖励过程 $MRP ⟨S, P_π, R_π, γ⟩$，求解基于该策略的价值函数 $v_π$。
  • 控制(control):已知一个马尔科夫决策过程MDP⟨S,A,P,R,γ⟩，求解最优价值函数v∗ 和 最优策略 π∗。

策略评估

含义

指计算给定策略下状态价值函数的过程
对策略评估，我们可 以使用同步迭代联合动态规划的算法:从任意一个状态价值函数开始，依据给定的策略，结合贝 尔曼期望方程、状态转移概率和奖励同步迭代更新状态价值函数，直至其收敛，得到该策略下最 终的状态价值函数

  • 贝尔曼期望方程给出了如何根据状态转换关系中的后续状态 s′ 来计算当前状态 s 的价值， 在同步迭代法中，我们使用上一个迭代周期 k 内的后续状态价值来计算更新当前迭代周期 k + 1
    内某状态 s 的价值
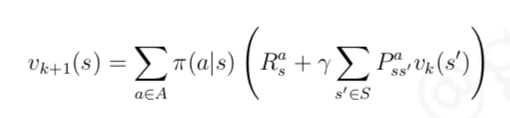
    • 我们可以对计算得到的新的状态价值函数再次进行迭代，直至状态函数收敛，也就是迭代计算得到每一个状态的新价值与原价值差别在一个很小的可接受范围内

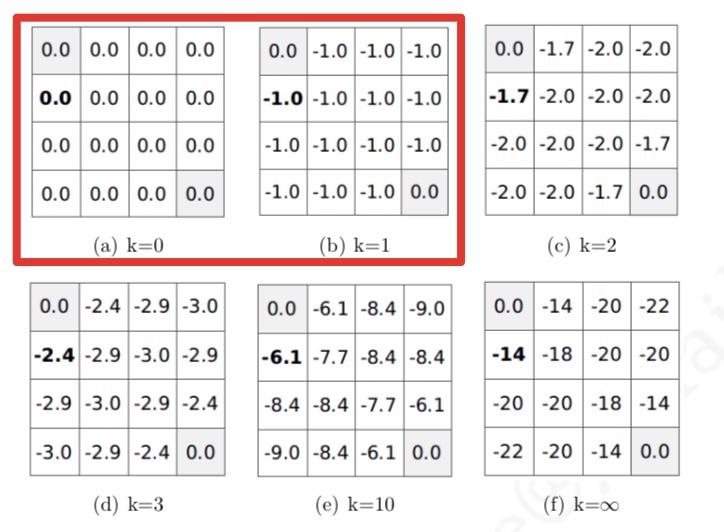
举例(小型方格世界迭代中的价值函数)

  • 均一概率的随机策略

策略迭代

背景

完成对一个策略的评估，将得到基于该策略下每一个状态的价值。很明显，不同状态对应的 价值一般也不同，那么个体是否可以根据得到的价值状态来调整自己的行动策略呢

迭代过程理解(贪婪策略)

个体在某个状态下选择的行为是其能够到达后续所有可能的状态中价值最 大的那个状态。我们以均一随机策略下第 2 次迭代后产生的价值函数为例说明这个贪婪策略

  • 新的贪婪策略比之前的均一随机策略要优秀不少，至少在靠近终止
    状态的几个状态中，个体将有一个明确的行为，而不再是随机行为了。我们从均一随机策略下的 价值函数中产生了新的更优秀的策略，这是一个策略改善的过程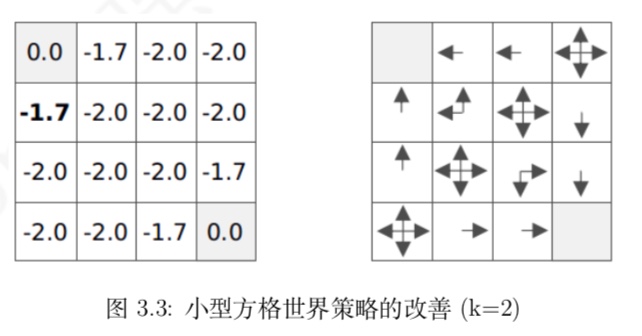

  • 我的理解：
    上面左图是各个状态的价值，右图是各个状态的策略，选择的贪婪策略由于各个状态不同的价值，导致了右图不同的策略。然后又由于不同的策略，执行下一步行动，继续会导致左图中不同的状态，以此循环

    • 依据新的策略 π′ 会得到一个新的价值函数，并产生新的贪婪策略，如此重复循环迭代将最 终得到最优价值函数 v∗ 和最优策略 π∗

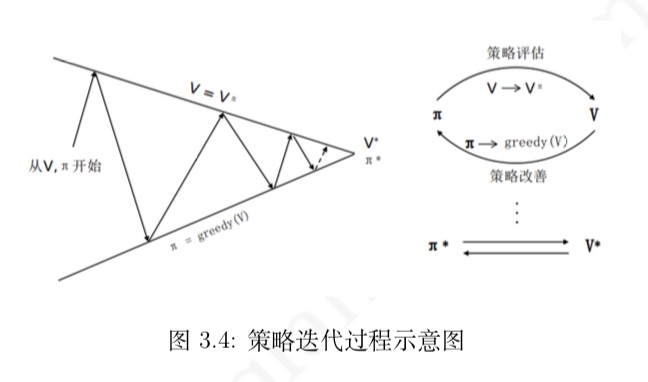
  • 策略迭代

    • 策略在循环迭代中得到更新改善的过程称为策略迭代
    • 从一个初始策略 π 和初始价值函数 V 开始，基于该策略进行完整的价值评估过程得到一个 新的价值函数，随后依据新的价值函数得到新的贪婪策略，随后计算新的贪婪策略下的价值函 数，整个过程反复进行，在这个循环过程中策略和价值函数均得到迭代更新，并最终收敛值最有 价值函数和最优策略

价值迭代

背景

细心的读者可能会发现，如果按照图 3.2 中第三次迭代得到的价值函数采用贪婪选择策略的 话，该策略和最终的最优价值函数对应的贪婪选择策略是一样的，它们都对应于最优策略，如图 3.5，而通过基于均一随机策略的迭代法价值评估要经过数十次迭代才算收敛。这会引出一个问 题:是否可以提前设置一个迭代终点来减少迭代次数而不影响得到最优策略呢?是否可以每迭代 一次就进行一次策略评估呢

最优策略的意义

  • 任何一个最优策略可以分为两个阶段:
    首先该策略要能产生当前状态下的最优行为，其次对 于该最优行为到达的后续状态时该策略仍然是一个最优策略

  • 直观感受(单纯的价值迭代)

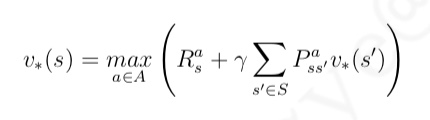
    这个公式带给我们的直觉是如果我们能知道最终状态的价值和相关奖励，可以直接计算得 到最终状态的前一个所有可能状态的最优价值。更乐观的是，即使不知道最终状态是哪一个状 态，也可以利用上述公式进行纯粹的价值迭代，不停的更新状态价值，最终得到最优价值，而且 这种单纯价值迭代的方法甚至可以允许存在循环的状态转换乃至一些随机的状态转换过程

举例

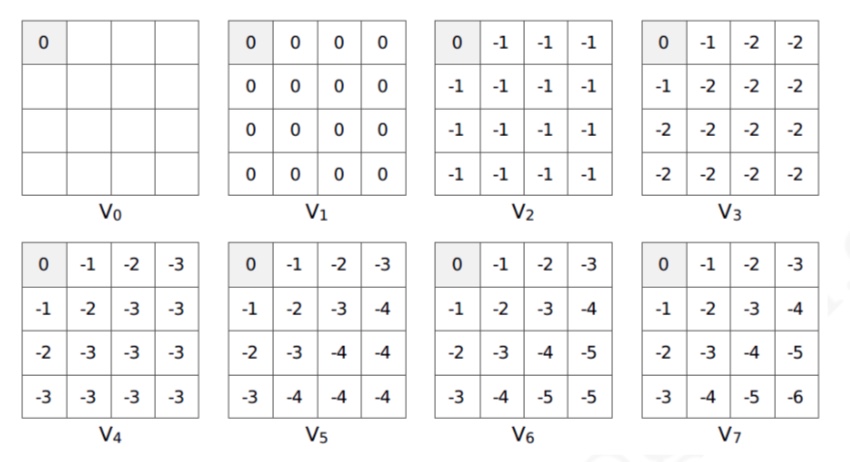
  • 首先考虑到个体知道环境的动力学特征的情形。在这种情况下，个体可以直接计算得到与终 止状态直接相邻(斜向不算)的左上角两个状态的最优价值均为 −1。随后个体又可以往右下角 延伸计算得到与之前最优价值为 −1 的两个状态香相邻的 3 个状态的最优价值为 −2。以此类推， 每一次迭代个体将从左上角朝着右下角方向依次直接计算得到一排斜向方格的最优价值，直至 完成最右下角的一个方格最优价值的计算
  • 个人理解：
    由于上面的直观感受可以知道，前一状态的最优价值可以由后一状态计算得到，所以从最终的终态出发，开始价值为0，然后倒推，得到每一个状态的最优价值（纯粹的价值迭代，并没有策略的参与）
  • 特点(注意并没有策略的参与)
    价值迭代的目标仍然是寻找到一个最优策略，它通过贝尔曼最优方程从前次迭代 的价值函数中计算得到当次迭代的价值函数，在这个反复迭代的过程中，并没有一个明确的策略 参与
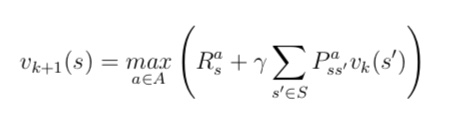
    • 需要 注意的是，在纯粹的价值迭代寻找最优策略的过程中，迭代过程中产生的状态价值函数不一定对 应一个策略。迭代过程中价值函数更新的公式为:

同步动态规划算法总结

使用同步动态规划进行规划基本就讲解完毕了。前文所述的这三类算法均是基于状态价值函数的

  • 其中迭代法策略评估属于预测问题，它使用贝尔曼期望方程来进行求解。
  • 策略迭代和价值迭代则属于控制问题
    • 其中前者使用贝尔曼 期望方程进行一定次数的价值迭代更新，随后在产生的价值函数基础上采取贪婪选择的策略改 善方法形成新的策略，如此交替迭代不断的优化策略;
    • 价值迭代则不依赖任何策略，它使用贝尔 曼最优方程直接对价值函数进行迭代更新

异步动态规划算法

前文所述的系列算法均为同步动态规划算法，它表示所有的状态更新是同步的。与之对应的 还有异步动态规划算法。在这些算法中，每一次迭代并不对所有状态的价值进行更新，而是依据 一定的原则有选择性的更新部分状态的价值

  • 这种算法能显著的节约计算资源，并且只要所有状 态能够得到持续的被访问更新，那么也能确保算法收敛至最优解。
  • 比较常用的异步动态规划思想 有:原位动态规划、优先级动态规划、和实时动态规划