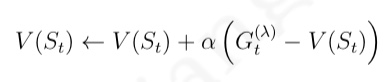背景
- 讲解如何解决一个可以被认为是 MDP、但却不掌握 MDP 具体细节(比如状态转移概率等等)的问题
- 从本章开始的连续两章内容将讲解如何解决一个可以被认为是 MDP、但却不掌握 MDP 具体细节的问题,也就是讲述个体如何在没有对环境动力学认识的模型的条件下如何直接 通过个体与环境的实际交互来评估一个策略的好坏或者寻找到最优价值函数和最优策略。其中 本章将聚焦于策略评估,也就是预测问题
蒙特卡罗强化学习 (Monte-Carlo reinforcement learning)
- MC:
指在不清楚 MDP 状态 转移概率的情况下,直接从经历完整的状态序列 (episode) 来估计状态的真实价值,并认为某状 态的价值等于在多个状态序列中以该状态算得到的所有收获的平均 - MC特点:
蒙特卡罗强化学习有如下特点:不依赖状态转移概率,直接从经历过的完整的状态序列中学习,使用的思想就是用平均收获值代替价值。理论上完整的状态序列越多,结果越准确 - 完整的状态序列 (complete episode):
指从某一个状态开始,个体与环境交互直到终止状态, 环境给出终止状态的奖励为止。- 完整的状态序列不要求起始状态一定是某一个特定的状态,但是 要求个体最终进入环境认可的某一个终止状态
- MC含义举例说明:
- 基于特定策略 π 的一个 Episode 信息可以表示为如下的一个序列:$S_1,A_1,R_2,S_2,A_2,…,S_t,A_t,R_{t+1},…,S_k ∼π$
- t 时刻状态 St 的收获可以表述为:
$G_t =R_{t+1} +γR_{t+2} +…+γ(T−1)R_T$ - 其中 T 为终止时刻。该策略下某一状态 s 的价值:
$v_π(s) = E_π[G_t|S_t = s]$
- 一个序列中出现多次状态的问题
- 如果一个完整的状态序列中某一需要计算的状态出现在序列的多个位置, 也就是说个体在与环境交互的过程中从某状态出发后又一次或多次返回过该状态,处理的两种方法:
- 首次访问:仅把状态序列中第一次出现该状 态时的收获值纳入到收获平均值的计算中
- 每次访问:针对一个状态序列中每次出现的该状态,都 计算对应的收获值并纳入到收获平均值的计算中
- 如果一个完整的状态序列中某一需要计算的状态出现在序列的多个位置, 也就是说个体在与环境交互的过程中从某状态出发后又一次或多次返回过该状态,处理的两种方法:
- 求解技巧
- 累进更新平均值(incremental mean)。而且这种计算平均值的思想也是强化学习的一 个核心思想之一
- 在求解状态收获的平均值的过程中,我们介绍一种非常实用的不需要存储所有历史收获的 计算方法:累进更新平均值(incremental mean)
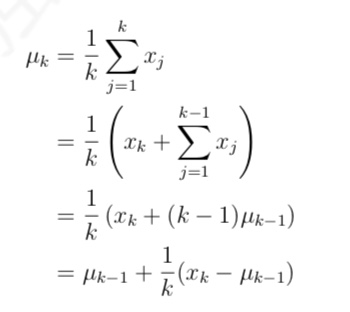
- 如果把该式中平均值和新数据分别看成是状态的价值和该状态的收获,那么该公式就变成了递增式的蒙特卡罗法更新状态价值。其公式如下:
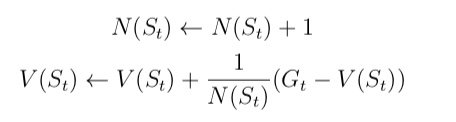
时序差分强化学习
- 定义:
指从采样得到的 不完整的状态序列学习,该方法通过合理的引导(bootstrapping),先估计某状态在该状态序列 完整后可能得到的收获,并在此基础上利用前文所属的累进更新平均值的方法得到该状态的价 值,再通过不断的采样来持续更新这个价值- 具体地说,在 TD 学习中,算法在估计某一个状态的收获时,用的是离开该状态的即刻奖励 $R_{t+1}$ 与下一时刻状态 $S_{t+1}$ 的预估状态价值乘以衰减系数 γ 组成:
$V(S_t) ← V(S_t) + α(R_{t+1} + γV(S_{t+1}) − V(S_t))$- 其中:$R_{t+1} + γV(S_{t+1}) 称为 TD 目标值。R_{t+1} + γV(S_{t+1}) − V(S_t)$称为 TD 误差
- 引导 (bootstrapping):指的是用 TD 目标值代替收获 $G_t$ 的过程
- 具体地说,在 TD 学习中,算法在估计某一个状态的收获时,用的是离开该状态的即刻奖励 $R_{t+1}$ 与下一时刻状态 $S_{t+1}$ 的预估状态价值乘以衰减系数 γ 组成:
MC,TD,DP比较
- MC,TD相同点:
- 不依赖于模型
- 它们都不再需要清楚某一状态的所有可能的后
续状态以及对应的状态转移概率 - 因此也不再像动态规划算法那样进行全宽度的回溯来更新状 态的价值。
- MC 和 TD 学习使用的都是通过个体与环境实际交互生成的一系列状态序列来更新 状态的价值。这在解决大规模问题或者不清楚环境动力学特征的问题时十分有效
- DP 算法则是基于模型的计算状态价值的方法,它通过计算一个状态 S 所 有可能的转移状态 S’ 及其转移概率以及对应的即时奖励来计算这个状态 S 的价值
- 是否使用引导数据:
- MC 学习并不使用引导数据,它使用实际产生的奖励值来计算状态 价值
- TD 和 DP 则都是用后续状态的预估价值作为引导数据来计算当前状态的价值
- 是否采样:
- MC 和 TD 不依赖模型,使用的都是个体与环境实际交互产生的采样 状态序列来计算状态价值的
- DP 则依赖状态转移概率矩阵和奖励函数,全宽度计算状态价 值,没有采样之说。
- MC算法
深度采样学习。一次学习完整经历,使用实际收获更新状态预估价值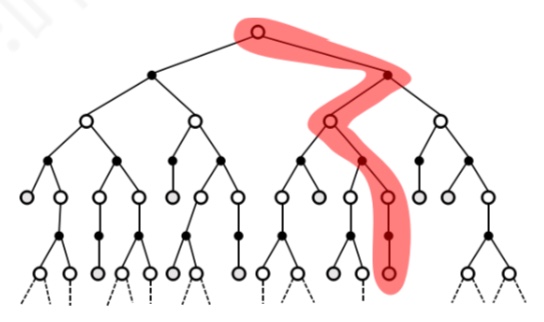
- TD 算法:
浅层采样学习。经历可不完整,使用后续状态的预估状态价值预估收获再更新当前状态价值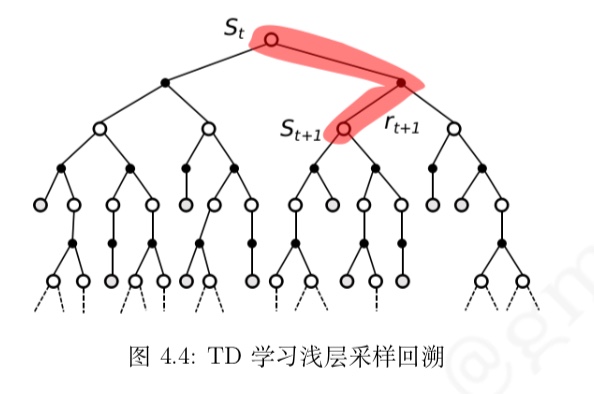
- DP算法:
浅层全宽度 (采样) 学习。依据模型,全宽度地使用后续状态预估价值来更新当前
状态价值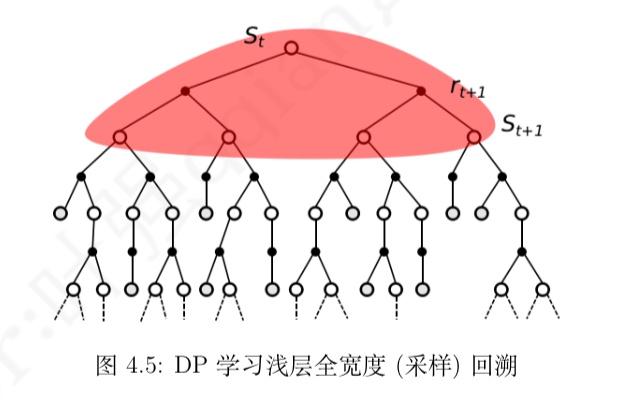
- 小结:
- 当使用单个采样,同时不经历完整的状态序 列更新价值的算法是 TD 学习;
- 当使用单个采样,但依赖完整状态序列的算法是 MC 学习;
- 当考虑全宽度采样,但对每一个采样经历只考虑后续一个状态时的算法是 DP 学习;
- 如果既考虑所 有状态转移的可能性,同时又依赖完整状态序列的,那么这种算法是穷举 (exhausive search) 法。
- 需要说明的是:DP 利用的是整个 MDP 问题的模型,也就是状态转移概率,虽然它并不实际利 用采样经历,但它利用了整个模型的规律,因此也被认为是全宽度 (full width) 采样的
n步时序差分学习简介
定义
- 第二节所介绍的 TD 算法实际上都是 TD(0) 算法,括号内的数字 0 表示的是在当前状态下 往前多看 1 步
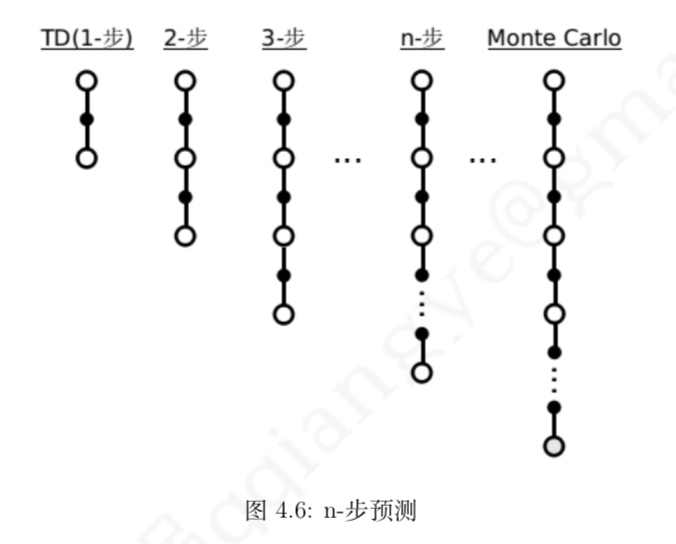

λ-收获
为了能在不增加计算复杂度的情况下综合考虑所有步数的预测,我们引入了一个新的参数 λ,并定义:λ-收获
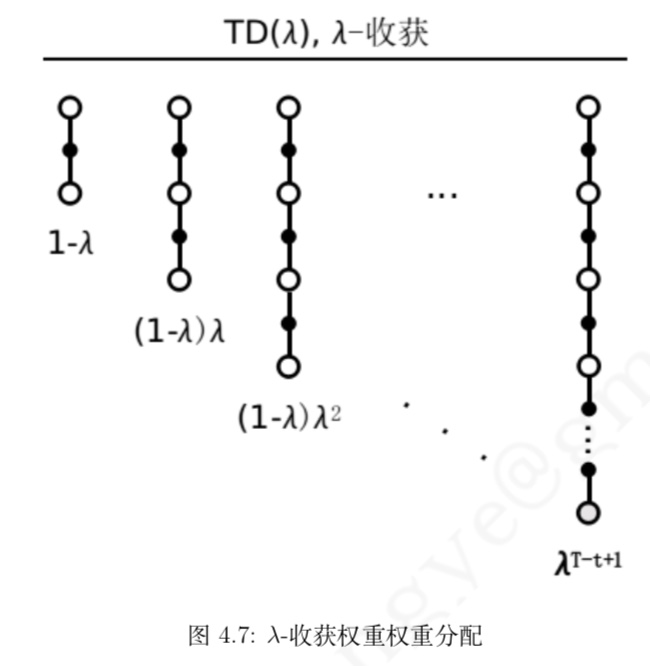
- 任意一个 n-步收获的权重被设计为 $(1 − λ)λ^{n−1}$,如图 4.7 所示。通过这样的权重设计,可以得到 λ-收获的计算公式为
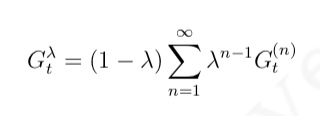
- 对应的 TD(λ) 被描述为