背景
问题的复杂性
- 本章之前的内容介绍的多是规模比较小的强化学习问题,生活中有许多实际问题要复杂得 多,有些是属于状态数量巨大甚至是连续的,有些行为数量较大或者是连续的。这些问题要是使 用前几章介绍的基本算法效率会很低,甚至会无法得到较好的解决
- 解决这类问题的常用方法是不再使用字典之类的查表式的方法来存储状态或行为的价值,而 是引入适当的参数,选取恰当的描述状态的特征,通过构建一定的函数来近似计算得到状态或行 为价值
- 在引入近似价值函数后,强化学习中不管是预测问题还是控制问题,就转变成近似函数的设 计以及求解近似函数参数这两个问题了
状态价值 $v_π(s)$ 的近似表示
如果能建立一个函数 vˆ, 这个函数由参数 w 描述,它可以直接接受表示状态特征的连续变量 s 作为输入,通过计算得到一个状态的价值,通过调整参数 w 的取值,使得其符合基于某一策略 π 的最终状态价值,那么这个函数就是状态价值 $v_π(s)$ 的近似表示
$\hat v{(s,w)} ≈ v_π(s)$行为价值 $q_π(s,a)$ 的近似表示
$\hat q(s,a,w) ≈ q_π(s,a)$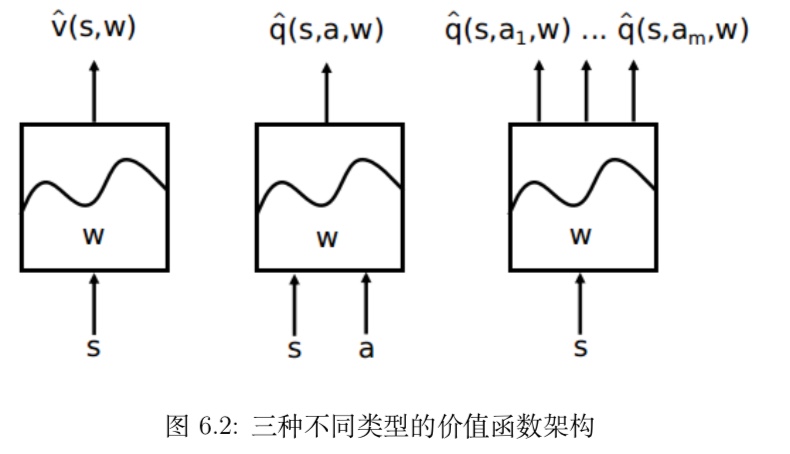
常用的近似价值函数(DQN算法)
理论上任何函数都可以被用作近似价值函数,实际选择何种近似函数需根据问题的特点。比较常用的近似函数有线性函数组合、神经网络、决策树、傅里叶变换等等,这里会重点介绍基于深度学习的神经网络计数进行特征表示,包括卷积神经网络。
DQN算法
DQN 算法主要使用经历回放 (experience replay) 来 实现价值函数的收敛。其具体做法为:
- 个体能记住既往的状态转换经历,对于每一个完整状态序 列里的每一次状态转换,
- 依据当前状态的 $st 价值以 ε-贪婪策略选择一个行为 a_t,执行该行为得 到奖励 r_{t+1} 和下一个状态 s_{t+1}$
- 将得到的状态转换存储至记忆中
- 当记忆中存储的容量足够大时,随机从记忆力提取一定数量的状态转换
- 用状态转换中下一状态来计算当前状态的目标价值,使用公式 (6.4) 计算目标价值与网络输出价值之间的均方差代价,使用小块梯度下降算法更 新网络的参数
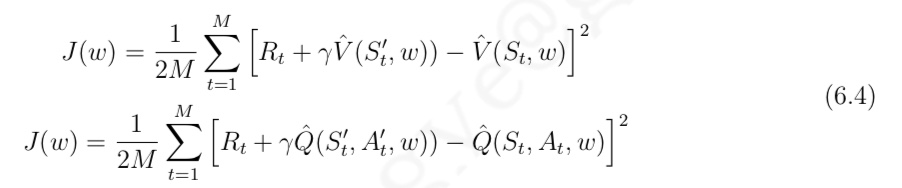
- 伪代码

- 该算法中 的状态 S 都由特征 φ(S) 来表示
DDQN(double deep Q network)
- 背景:
DQN得了不俗的成绩,不过其并不能保证一直收敛,研究表明这种估计目标价值的算法过于乐观的高 估了一些情况下的行为价值,导致算法会将次优行为价值一致认为最优行为价值,最终不能收敛 至最佳价值函数 - 和DQN区别
该算法使用两个架构相同的近似价值函数:- 其中一个用来根据策略生成交互行为并随 时频繁参数 (θ)
- 另一个则用来生成目标价值, 其参数 (θ−) 每隔一定的周期进行更新。该算法绝 大多数流程与 DQN 算法一样,只是在更新目标价值时使用公式 (6.20):
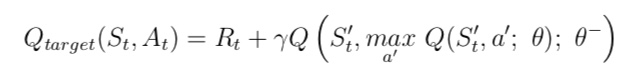
- 该式表明,DDQN 在生成目标价值时使用了生成交互行为并频繁更新参数的价值网络 Q(θ), 在这个价值网络中挑选状态 S′下最大价值对应的行为 $A′_t$,随后再用状态行为对 $(S_t′, A′_t)$ 代入目标价值网络 Q(θ−) 得出目标价值。实验表明这样的更改比 DQN 算法更加稳定,更容易收敛值 最优价值函数和最优策略
- 同样存在深度学习的问题
在使用神经网络等深度学习技术来进行价值函数近似时,有可能会碰到无法得到预期结果的情况,深度学习的问题这里也会遇到