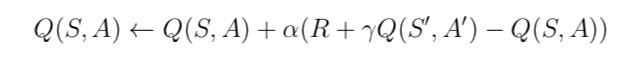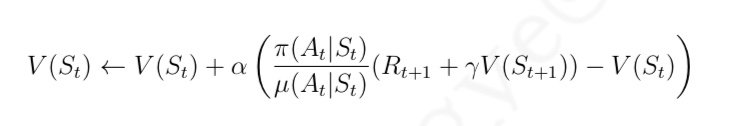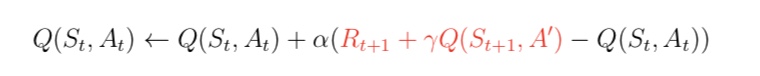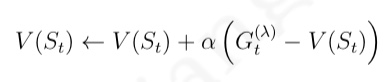什么是相似信息的推荐模型

• 定义
  相似信息的推荐模型又叫“临近”（Neighborhood）模型。顾名思义，就是我们希望利用临近、或者相似的数据点来为用户推荐。
• 协同过滤
  临近模型的内在假设是推荐系统中著名的“协同过滤”（Collaborative Filtering）
  • 相似的用户可能会有相似的喜好，相似的物品可能会被相似的人所偏好。
  • 于是，如果我们能够定义怎么寻找相似的用户或者相似的物品，那么我们就可以利用这些类别的人群或者物品来给用户进行推荐。

• 举例
  A,B都看了战狼2，B还看了红海，那么就给A推荐红海
  思考过程：
  • 第一，联系用户 A 和用户 B 的是他们都看过《战狼 2》。这就帮助我们定义了 A 和 B 是相似用户
  • 第二，我们的假定是，相似的用户有相似的观影偏好，于是我们就直接把 B 的另外一个观看过的电影《红海行动》拿来推荐给了 A
  • 意义：
  • 这两个步骤其实就很好地解释了“协同过滤”中“协同”的概念，意思就是相似的用户互相协同，互相过滤信息
  • “协同过滤”从统计模型的意义上来讲，其实就是“借用数据”，在数据稀缺的情况下帮助建模。掌握这个思路是非常重要的建模手段
  • 在用户 A 数据不足的情况下，我们挖掘到可以借鉴用户 B 的数据
    • 因此，我们其实是把用户 A 和用户 B“聚类”到了一起，认为他们代表了一个类型的用户。
    • 当我们把对单个用户的建模抽象上升到某一个类型的用户的时候，这就把更多的数据放到了一起

基于相似用户的协同过滤

如何才能够比较系统地定义这样的流程呢？

• 首先，问题被抽象为我们需要估计用户 I 针对一个没有“触碰过”（这里指点击、购买、或者评分等行为）的物品 J 的偏好
  • 第一步，我们需要构建一个用户集合，这个用户集合得满足两个标准：
    • 第一，这些用户需要已经触碰过物品 J，这是与用户 I 的一大区别；
    • 第二，这些用户在其他的行为方面需要与用户 I 类似
  • 然后进行打分
    • 简单的做法
      首先，我们已经得到了所有和 I 相似的用户对 J 的打分。那么，一种办法就是，直接用这些打分的平均值来预估 J 的评分。也就是说，如果我们认为这个相似集合都是和用户 I 相似的用户，那么他们对 J 的偏好，我们就认为是 I 的偏好。显然这是一个很粗糙的做法
    • 改进方法
      • 采用加权平均的做法
        也就是说，和用户 I 越相似的用户，我们越倚重这些人对 J 的偏好
      • 我们也需要对整个评分进行一个修正
        • 虽然这个相似集合的人都对 J 进行过触碰，但是每个人的喜好毕竟还是不一样的。比如有的用户可能习惯性地会对很多物品有很强的偏好。因此，仅仅是借鉴每个人的偏好，而忽略了这些用户的偏差，这显然是不够的。所以，我们需要对这些评分做这样的修正，那就是减去这些相似用户对所有东西的平均打分，也就是说，我们需要把这些用户本人的偏差给去除掉
  • 方法总结：
    综合刚才说的两个因素，可以得到一个更加合适的打分算法，那就是，用户 I 对物品 J 的打分来自两个部分：
    • 一部分是 I 的平均打分
    • 另外一部分是 I 对于 J 的一个在平均打分之上的补充打分
      • 这个补充打分来自于刚才我们建立的相似用户集，是这个相似用户集里每个用户对于 J 的补充打分的一个加权平均
        • 权重依赖于这个用户和 I 的相似度
        • 每个用户对于 J 的补充打分是他们对于 J 的直接打分减去他们自己的平均打分

相似信息的构建

几个关键要素：

• 我们怎么来定义两个用户是相似的
  • 一种最简单的办法，就是计算两个用户对于他们都偏好物品的“皮尔森相关度”（Pearson Correlation）
  • 皮尔森相关度是针对每一个“两个用户”都同时偏好过的物品，看他们的偏好是否相似，这里的相似是用乘积的形式出现的。当两个偏好的值都比较大的时候，乘积也就比较大
• 设定一些“阈值”来筛选刚才所说的相关用户集合
  • 我们可以设置最多达到前 K 个相似用户（比如 K 等于 100 或者 200）
• 加权平均里面的权重问题
  • 一种权重，就是直接使用两个用户的相似度，也就是我们刚计算的皮尔森相关度
    • 当然，这里有一个问题，如果直接使用，我们可能会过分“相信”有一些相关度高但自身数据也不多的用户
    • 所以我们可以把皮尔森相关度乘以一个系数，这个系数是根据自身的偏好数量来定的

总结

• 协同过滤
  相似的用户可能会有相似的喜好，相似的物品可能会被相似的人所偏好
• 基于相似用户协同过滤
  • 问题被抽象为我们需要估计用户 I 针对一个没有“触碰过”（这里指点击、购买、或者评分等行为）的物品 J 的偏好
  • 假设已经构建了这样的用户组，然后就是对需要推荐的物品进行打分，有分为简单的平均打分，和加权打分等
• 相似信息的构建(皮尔森相似度，设置阈值构建用户集合)

最简单的流行度估计

• 定义
  什么是基于流行度（Popularity-based）？通俗地讲，就是什么内容吸引用户，就给用户推荐什么内容

  • 隐含假设：就是物品质量的好坏和流行度成正比例关系

• 流行度常见影响因素
  不能简单看流量或者点击的绝对量来评价

  • 时间
    比如用户对新闻的观看时间一般是有规律的，所以会影响绝对数据
  • 位置
    物品显示的位置也会影响绝对数据

• 如何衡量

  • 采用比值Ratio,或者某种可能性
    • 比如点击率，但是点击率估计所需要的数据依赖会收到时间和位置的偏差的影响，所以如何构建无偏差数据呢？

• 构建无偏差数据(点击率)
  本身就是一个负责的问题，这里举简单的解放办法：

  • EE算法(Exploitation & Exploration)(epsilon贪心算法)
    就是将流量分为两部分，一部分随机显示物品，然后基于这部分流量计算流行度，第二部分跟进这个流行度来显示物品

对点击率建模

如果从数学上对点击率建模，其实可以把一个物品在显示之后是否被点击看成是一个“伯努利随机变量”，于是对点击率的估计，就变成了对一个伯努利分布参数估计的过程

• 最大似然估计(Maximum Likelihood Estimation)
  • 定义
    就是说，希望找到参数的取值可以最大限度地解释当前的数据
    • 这个估计的数值就是某个物品当前的点击总数除以被显示的次数。通俗地讲，如果我们显示某个物品 10 次，被点击了 5 次，那么在最大似然估计的情况下，点击率的估计值就是 0.5
  • 弊端
    如果我们并没有显示当前的物品，那么，最大似然估计的分母就是 0；如果当前的物品没有被点击过，那么分子就是 0
    • 在这两种情况下，最大似然估计都无法真正体现出物品的流行度

高级流行度估计

我们从统计学的角度来讲了讲，如何利用最大似然估计法来对一个伯努利分布所代表的点击率的参数进行估计。这里面的第一个问题就是刚才我们提到的分子或者分母为 0 的情况。显然，这种情况下并不能很好地反应这些物品的真实属性

• 先验信息(解决方案之一)
  虽然我们现在没有显示这个物品或者这个物品没有被点击，但是，我们“主观”地认为，比如说在显示 100 次的情况下，会有 60 次的点击

  • 注意，这些显示次数和点击次数都还没有发生
  • 在这样的先验概率的影响下，点击率的估计，或者说得更加精确一些，点击率的后验概率分布的均值，就成为了实际的点击加上先验的点击，除以实际的显示次数加上先验的显示次数。
  • 你可以看到，在有先验分布的情况下，这个比值永远不可能为 0
    • 利用先验信息来“平滑”（Smooth）概率的估计，是贝叶斯统计（Bayesian Statistics）中经常使用的方法
  • 如果用更加精准的数学语言来表述这个过程，我们其实是为这个伯努利分布加上了一个 Beta 分布的先验概率，并且推导出了后验概率也是一个 Beta 分布。这个 Beta 分布参数的均值，就是我们刚才所说的均值

• 时间折扣(基于前后时间关联)(另一种方法)
  每个时段的估计和前面的时间是有一定关联的。这也就提醒我们是不是可以用之前的点击信息，来更加准确地估计现在这个时段的点击率

  • 一种最简单的方法还是利用我们刚才所说的先验概率的思想
    • 那就是，当前 T 时刻的点击和显示的先验数值是 T-1 时刻的某种变换
      • 比如早上 9 点到 10 点，某个物品有 40 次点击，100 次显示。那么 10 点到 11 点，我们在还没有显示的情况下，就可以认为这个物品会有 20 次点击，50 次显示。注意，我们把 9 点到 10 点的真实数据乘以 0.5 用于 10 点到 11 点的先验数据
    • 这种做法是一种主观的做法。而且是否乘以 0.5 还是其他数值需要取决于测试。但是这种思想，有时候叫作“时间折扣”（Temporal Discount），是一种非常普遍的时序信息处理的手法

总结

• 我们简要介绍了为什么需要基于流行度进行推荐
• 我们详细介绍了如何对流行度进行估计以及从统计角度看其含义
• 我们简要地提及了一些更加高级的流行度估计的方法

极客时间版权所有

强化学习路在何方

深度强化学习的泡沫

背景

• 2015年，DeepMind的Volodymyr Mnih等研究员在《自然》杂志上发表论文Human-level control through deep reinforcement learning[1]，该论文提出了一个结合深度学习（DL）技术和强化学习（RL）思想的模型Deep Q-Network(DQN)，在Atari游戏平台上展示出超越人类水平的表现。自此以后，结合DL与RL的深度强化学习（Deep Reinforcement Learning, DRL）迅速成为人工智能界的焦点
• 过去三年间，DRL算法在不同领域大显神通，DeepMind负责AlphaGo项目的研究员David Silver喊出“AI = RL + DL”，认为结合了DL的表示能力与RL的推理能力的DRL将会是人工智能的终极答案

DRL的可复现性危机

• 由于发表的文献中往往不提供重要参数设置和工程解决方案的细节，很多算法都难以复现，RL专家直指当前DRL领域论文数量多却水分大、实验难以复现等问题。该文在学术界和工业界引发热烈反响。很多人对此表示认同，并对DRL的实际能力产生强烈怀疑
  • 针对DRL领域，Pineau展示了该研究组对当前不同DRL算法的大量可复现性实验。实验结果表明，不同DRL算法在不同任务、不同超参数、不同随机种子下的效果大相径庭

DRL研究存在多少坑

2018年的情人节当天，曾经就读于伯克利人工智能研究实验室的Alexirpan通过一篇博文Deep Reinforcement Learning Doesn’t Work Yet[13]给DRL圈送来了一份苦涩的礼物，从实验角度总结了DRL算法存在的几大问题：

• 样本利用率非常低；
• 最终表现不够好，经常比不过基于模型的方法；
• 好的奖励函数难以设计；
• 难以平衡 “ 探索 ” 和 “ 利用 ” ,以致算法陷入局部极小；
• 对环境的过拟合；
• 灾难性的不稳定性…

负面评论还将持续发酵。那么， DRL的问题根结在哪里？前景真的如此黯淡吗？如果不与深度学习结合，RL的出路又在哪里？

免模型强化学习的本质缺陷

RL分类

RL算法可以分为基于模型的方法（Model-based）与免模型的方法（Model-free）

• 前者主要发展自最优控制领域。通常先通过高斯过程（GP）或贝叶斯网络（BN）等工具针对具体问题建立模型，然后再通过机器学习的方法或最优控制的方法，如模型预测控制（MPC）、线性二次调节器（LQR）、线性二次高斯（LQG）、迭代学习控制（ICL）等进行求解
• 而后者更多地发展自机器学习领域，属于数据驱动的方法。算法通过大量采样，估计代理的状态、动作的值函数或回报函数，从而优化动作策略

免模型缺陷

• Ben Recht连发了13篇博文，从控制与优化的视角，重点探讨了RL中的免模型方法[18]。Recht指出免模型方法自身存在以下几大缺陷
  • 免模型方法无法从不带反馈信号的样本中学习，而反馈本身就是稀疏的，因此免模型方向样本利用率很低，而数据驱动的方法则需要大量采样
    • 比如在Atari平台上的《Space Invader》和《Seaquest》游戏中，智能体所获得的分数会随训练数据增加而增加。利用免模型DRL方法可能需要 2 亿帧画面才能学到比较好的效果。AlphaGo 最早在 Nature 公布的版本也需要 3000 万个盘面进行训练。而但凡与机械控制相关的问题，训练数据远不如视频图像这样的数据容易获取，因此只能在模拟器中进行训练。而模拟器与现实世界间的Reality Gap，直接限制了训练自其中算法的泛化性能。另外，数据的稀缺性也影响了其与DL技术的结合
  • 免模型方法不对具体问题进行建模，而是尝试用一个通用的算法解决所有问题。而基于模型的方法则通过针对特定问题建立模型，充分利用了问题固有的信息。免模型方法在追求通用性的同时放弃这些富有价值的信息
  • 基于模型的方法针对问题建立动力学模型，这个模型具有解释性。而免模型方法因为没有模型，解释性不强，调试困难
  • 相比基于模型的方法，尤其是基于简单线性模型的方法，免模型方法不够稳定，在训练中极易发散

通过Recht的分析，我们似乎找到了DRL问题的根结。近三年在机器学习领域大火的DRL算法，多将免模型方法与DL结合，而免模型算法的天然缺陷，恰好与Alexirpan总结的DRL几大问题相对应

为什么多数DRL的工作都是基于免模型方法呢

• 免模型的方法相对简单直观，开源实现丰富，比较容易上手
• 当前RL的发展还处于初级阶段，学界的研究重点还是集中在环境是确定的、静态的，状态主要是离散的、静态的、完全可观察的，反馈也是确定的问题（如Atari游戏）上。针对这种相对“简单”、基础、通用的问题，免模型方法本身很合适
• 绝大多数DRL方法是对DQN的扩展，属于免模型方法

基于模型或免模型，问题没那么简单

基于模型的方法，未来潜力巨大

基于模型的方法一般先从数据中学习模型，然后基于学到的模型对策略进行优化。学习模型的过程和控制论中的系统参数辨识类似

• 因为模型的存在，基于模型的方法可以充分利用每一个样本来逼近模型，数据利用率极大提高
• 基于模型的方法则在一些控制问题中，相比于免模型方法，通常有10^2级的采样率提升。
• 此外，学到的模型往往对环境的变化鲁棒,当遇到新环境时，算法可以依靠已学到的模型做推理，具有很好的泛化性能
• 预测学习（Predictive Learning)关系
  基于模型的方法还与潜力巨大的预测学习（Predictive Learning）紧密相关。由于建立了模型，本身就可以通过模型预测未来，这与Predictive Learning的需求不谋而合
  • 基于模型的RL方法可能是实现Predictive Learning的重要技术之一

基于模型问题也较多，免模型方法，依旧是第一选择

基于模型的DRL方法相对而言不那么简单直观，RL与DL的结合方式相对更复杂，设计难度更高。目前基于模型的DRL方法通常用高斯过程、贝叶斯网络或概率神经网络（PNN）来构建模型
基于模型的方法也还若干自身缺陷

• 针对无法建模的问题束手无策
• 建模会带来误差，而且误差往往随着算法与环境的迭代交互越来越大，使得算法难以保证收敛到最优解
• 模型缺乏通用性，每次换一个问题，就要重新建模
• 可能的工作，笔者认为
  • 我们可以考虑多做一些基于模型的DRL方面的工作，克服当前DRL存在的诸多问题
  • 此外，还可以多研究结合基于模型方法与免模型方法的半模型方法，兼具两种方法的优势
    • 这方面经典的工作有RL泰斗Rich Sutton提出的Dyna框架和Dyna-2框架[28]

其他问题

• 模拟器存在非常大的问题，经过调试的线性策略就已经可以取得非常好的效果——这样的模拟器实在过于粗糙，难怪基于随机搜索的方法可以在同样的模拟器上战胜免模型方法
  • 可见目前RL领域的实验平台还非常不成熟，在这样的测试环境中的实验实验结果没有足够的说服力。很多研究结论都未必可信
• 一些学者指出当前RL算法的性能评判准则也不科学

重新审视强化学习

• DQN和AlphaGo系列工作给人留下深刻印象，但是这两种任务本质上其实相对“简单”。因为这些任务的环境是确定的、静态的，状态主要是离散的、静态的、完全可观察的，反馈是确定的，代理也是单一的
• 目前DRL在解决部分可见状态任务（如StarCraft），状态连续的任务（如机械控制任务），动态反馈任务和多代理任务中还没取得令人惊叹的突破

重新审视RL的研究(或不足)(值得研究的方向)

机器学习是个跨学科的研究领域，而RL则是其中跨学科性质非常显著的一个分支。RL理论的发展受到生理学、神经科学和最优控制等领域的启发，现在依旧在很多相关领域被研究

• 基于模型的方法
  如上文所述，基于模型的方法不仅能大幅降低采样需求，还可以通过学习任务的动力学模型，为预测学习打下基础
• 提高免模型方法的数据利用率和扩展性
  这是免模型学习的两处硬伤，也是Rich Sutton的终极研究目标。这个领域很艰难，但是任何有意义的突破也将带来极大价值
• 更高效的探索策略（Exploration Strategies）
  平衡“探索”与“利用”是RL的本质问题，这需要我们设计更加高效的探索策略。除了若干经典的算法如Softmax、ϵ-Greedy[1]、UCB[72]和Thompson Sampling[73]等，近期学界陆续提出了大批新算法，如Intrinsic Motivation [74]、Curiosity-driven Exploration[75]、Count-based Exploration [76]等。其实这些“新”算法的思想不少早在80年代就已出现[77]，而与DL的有机结合使它们重新得到重视。此外，OpenAI与DeepMind先后提出通过在策略参数[78]和神经网络权重[79]上引入噪声来提升探索策略, 开辟了一个新方向
• 与模仿学习（Imitation Learning, IL）结合
  机器学习与自动驾驶领域最早的成功案例ALVINN[33]就是基于IL；当前RL领域最顶级的学者Pieter Abbeel在跟随Andrew Ng读博士时候,设计的通过IL控制直升机的算法[34]成为IL领域的代表性工作.IL介于RL与监督学习之间，兼具两者的优势，既能更快地得到反馈、更快地收敛，又有推理能力，很有研究价值
• 奖赏塑形（Reward Shaping）
  奖赏即反馈，其对RL算法性能的影响是巨大的。
  • Alexirpan的博文中已经展示了没有精心设计的反馈信号会让RL算法产生多么差的结果
  • 设计好的反馈信号一直是RL领域的研究热点
  • 近年来涌现出很多基于“好奇心”的RL算法和层级RL算法
    • 这两类算法的思路都是在模型训练的过程中插入反馈信号，从而部分地克服了反馈过于稀疏的问题。
  • 另一种思路是学习反馈函数，这是逆强化学习（Inverse RL, IRL）的主要方式之一。
    • 近些年大火的GAN也是基于这个思路来解决生成建模问题, GAN的提出者Ian Goodfellow也认为GAN就是RL的一种方式 [36]。而将GAN于传统IRL结合的GAIL[37]已经吸引了很多学者的注意
• RL中的迁移学习与多任务学习
  当前RL的采样效率极低，而且学到的知识不通用。迁移学习与多任务学习可以有效解决这些问题
• 提升RL的的泛化能力
  • 机器学习最重要的目标就是泛化能力, 而现有的RL方法大多在这一指标上表现糟糕[8]，无怪乎Jacob Andreas会批评RL的成功是来自“train on the test set”
  • 研究者们试图通过学习环境的动力学模型[80]、降低模型复杂度[29]或模型无关学习[81]来提升泛化能力，这也促进了基于模型的方法与元学习（Meta-Learning）方法的发展
• 层级RL（Hierarchical RL, HRL）
• 与序列预测（Sequence Prediction）结合
  • Sequence Prediction与RL、IL解决的问题相似又不相同。三者间有很多思想可以互相借鉴
• 免模型方法探索行为的安全性（Safe RL）
  • 相比于基于模型的方法，免模型方法缺乏预测能力，这使得其探索行为带有更多不稳定性。一种研究思路是结合贝叶斯方法为RL代理行为的不确定性建模，从而避免过于危险的探索行为
• 关系RL
  近期学习客体间关系从而进行推理与预测的“关系学习”受到了学界的广泛关注。关系学习往往在训练中构建的状态链，而中间状态与最终的反馈是脱节的
• 对抗样本RL
• 处理其他模态的输入

重新审视RL的应用

RL只能打游戏、下棋，其他的都做不了？

• 我们不应对RL过于悲观。其实能在视频游戏与棋类游戏中超越人类，已经证明了RL推理能力的强大。通过合理改进后，有希望得到广泛应用
• 控制领域
  这是RL思想的发源地之一，也是RL技术应用最成熟的领域。控制领域和机器学习领域各自发展了相似的思想、概念与技术，可以互相借鉴
• 自动驾驶领域
  驾驶就是一个序列决策过程，因此天然适合用RL来处理
• NLP领域
  相比于计算机视觉领域的任务，NLP领域的很多任务是多轮的，即需通过多次迭代交互来寻求最优解（如对话系统）；而且任务的反馈信号往往需要在一系列决策后才能获得（如机器写作）。这样的问题的特性自然适合用RL来解决
  • 因而近年来RL被应用于NLP领域中的诸多任务中，如文本生成、文本摘要、序列标注、对话机器人（文字/语音）、机器翻译、关系抽取和知识图谱推理等等
• 推荐系统与检索系统领域
  RL中的Bandits系列算法早已被广泛应用于商品推荐、新闻推荐和在线广告等领域。近年也有一系列的工作将RL应用于信息检索、排序的任务中
• 金融领域
  RL强大的序列决策能力已经被金融系统所关注。无论是华尔街巨头摩根大通还是创业公司如Kensho，都在其交易系统中引入了RL技术
• 对数据的选择
  在数据足够多的情况下，如何选择数据来实现“快、好、省”地学习，具有非常大的应用价值
• 通讯、生产调度、规划和资源访问控制等运筹领域
  这些领域的任务往往涉及“选择”动作的过程，而且带标签数据难以取得，因此广泛使用RL进行求解

总结

• 虽然有上文列举的诸多成功应用，但我们依旧要认识到，当前RL的发展还处于初级阶段，不能包打天下。目前还没有一个通用的RL解决方案像DL一样成熟到成为一种即插即用的算法。RL算法的输出存在随机性，这是其“探索”哲学带来的本质问题，因此我们不能盲目 All in RL, 也不应该RL in All

广义的RL——从反馈学习

定义与意义

• 本节使用“广义的RL”一词指代针对“从反馈学习”的横跨多个学科的研究。与上文中介绍的来自机器学习、控制论、经济学等领域的RL不同，本节涉及的学科更宽泛，一切涉及从反馈学习的系统，都暂且称为广义的RL
• 行为和反馈是智能形成的基石
  • 生成论（Enactivism）认为行为是认知的基础，行为与感知是互相促进的，智能体通过感知获得行为的反馈，而行为则带给智能体对环境的真实有意义的经验[65]。

广义的RL，是未来一切机器学习系统的形式

只要一个机器学习系统会通过接收外部的反馈进行改进，这个系统就不仅仅是一个机器学习系统，而且是一个RL系统。当前在互联网领域广为使用的A/B测试就是RL的一种最简单的形式。而未来的机器学习系统，都要处理分布动态变化的数据并从反馈中学习。因此可以说，我们即将处于一个“一切机器学习都是RL”的时代，学界和工业界都亟需加大对RL的研究力度

广义的RL，是很多领域研究的共同目标

节已经提到RL在机器学习相关的领域被分别发明与研究，其实这种从反馈中学习的思想，在很多其他领域也被不断地研究。仅举几例如下

• 在心理学领域，经典条件反射与操作性条件反射的对比
• 在教育学领域，一直有关于“主动学习”与“被动学习”两种方式的对比与研究
• 在组织行为学领域，学者们探究“主动性人格”与“被动性人格”的不同以及对组织的影响
• 在企业管理学领域，企业的“探索式行为”和“利用式行为”一直是一个研究热点

可以说，一切涉及通过选择然后得到反馈，然后从反馈中学习的领域，几乎都有RL的思想以各种形式存在，因此笔者称之为广义的RL

• 这些学科为RL的发展提供了丰富的研究素材，积累了大量的思想与方法。同时，RL的发展不会仅仅对人工智能领域产生影响，也会推动广义的RL所包含的诸多学科共同前进。

束语

• 虽然RL领域目前还存在诸多待解决的问题，在DRL这一方向上也出现不少泡沫，但我们应该看到RL领域本身在研究和应用领域取得的长足进步
• 这一领域值得持续投入研究，但在应用时需保持理性
• 而对基于反馈的学习的研究，不仅有望实现人工智能的最终目标，也对机器学习领域和诸多其他领域的发展颇有意义
• 这确实是通向人工智能的最佳路径。这条路上布满荆棘，但曙光已现

背景

• 前面的算法都是与真实的环境进行交互，个体并不试图去理解环境动力学
• 如果能构建一个较为准确地模拟环境动力学特 征的模型或者问题的模型本身就类似于一些棋类游戏是明确或者简单的，个体就可以通过构建这样的模型来模拟其与环境的交互，这种依靠模型模拟而不实际与环境交互的过程类似于“思考”过程
  • 通过思考，个体可以对问题进行规划、在与环境实际交互时搜索交互可能产生的各种 后果并从中选择对个体有利的结果
    • 我理解是通过模拟的环境，得到各自行为，然后与真实环境进行交互的时候，从这些模拟环境得到的行为中搜索，选择最优的结果

环境的模型

模型是个体构建的对于环境动力学特征的表示

基于模型的强化学习流程

• 当个体得到了一 个较为准确的描述环境动力学的模型时，它在与环境交互的过程中，既可以通过实际交互来提高模型的准确程度，也可以在交互间隙利用构建的模型进行思考、规划，决策出对个体有力的行为

  

• 学习一个模型相当于丛经历 $S_1, A_1, R_2, . . . , S_T$ 中通过监督学习得到一个模型 $M_η$

  • 训练数据为
    $S_1,A_1 →R_2,S_2$
    $S_2,A_2 →R_3,S_3$..
    $S_{T−1},A_{T−1} →R_T,S_T$

• 使用近似的模型解决强化学习问题与使用价值函数或策略函数的近似表达来解决强化学习问题并不冲突，它们是从不同角度来近似求解一个强化学习问题

  • 当构建一个模型比构建近似价值函数 或近似策略函数更方便时，那么使用近似模型来求解会更加高效

• 特别注意模型参数要随着个体与环境交互而不断地动态更新，即通过实际经历要与使用模型产生的虚拟经历相结合来解决问题

  • 这就催生了一类整合了学习与规划的强化学习算法——Dyna

Dyna算法(整合学习与规划)

• Dyna 算法从实际经历中学习得到模型，同时联合使用实际经历和基于模型采样得到的虚拟经历来学习和规划，更新价值和 (或) 策略函数
• 伪代码
  • 我的理解：
    • 从开始是通过真实环境去得到模型环境Model
    • 下面会使用Model得到虚拟的经历，结合上面真实经历来更新Q(S,A)

基于模拟的搜索

• 前向搜索形式
  在强化学习中，基于模拟的搜索 (simulation-based search) 是一种前向搜索形式,它从当前 时刻的状态开始，利用模型来模拟采样，构建一个关注短期未来的前向搜索树，将构建得到的搜索树作为一个学习资源，使用不基于模型的强化学习方法来寻找当前状态下的最优策略
  • 我的理解就是通过模型来构造一颗状态行为树，然后搜索在当前状态下的最优行为，也就是最优策略
• 如果使用蒙特卡罗学习方法则称为蒙特卡罗搜索，如果使用 Sarsa 学习方法，则称为 TD 搜索

背景

• 在行为空间规模庞大或者是连续行为的情况下，基于价值的强化学习将很难学习到一个好的结果，这种情况下可以直接进行策略的学习

  • 即将策略看成是状态和行为的带参数的策略函 数，通过建立恰当的目标函数、利用个体与环境进行交互产生的奖励来学习得到策略函数的参数。
  • 策略函数针对连续行为空间将可以直接产生具体的行为值，进而绕过对状态的价值的学习

• 在实际应用中通过建立分别对于状态价值的近似函数和策略函数

  • 使得一方面可以基于价值函 数进行策略评估和优化
  • 另一方面优化的策略函数又会使得价值函数更加准确的反应状态的价 值，两者相互促进最终得到最优策略

基于策略学习的意义

背景

基于价值的强化学习虽然能出色地解决很多问题，但面对行为空间连续、观测受 限、随机策略的学习等问题时仍然显得力不从心

• 问题1(行为空间连续)

  • 基于近似价值函数的学习可以较高效率地解决连续状态空间的强化学习问题，但其行为空间仍然是离散的
  • 如果行为空间是连续的，可以认为单纯基于价值函数近似的强化 学习无法解决连续行为空间的问题，其中每一 个方向上的分量可以是 [-1,1] 之间的任何连续值。在这个例子 (图 7.1) 中，行为由两个特征来描 述，其中每一个特征具体的值是连续的。比如：

• 问题2(观测受限)

  • 此外，在使用特征来描述状态空间中的某一个状态时，有可能因为个体观测的限制或者建 模的局限，导致本来不同的两个状态却拥有相同的特征描述，进而导致无法得到最优解
    • 在这种情况下，由于个体对于状态观测的特征不够多，导致了多个状 态发生重名情况，进而导致基于价值的学习得不到最优解

• 问题3(随机策略的学习)

  • 基于价值的学习对应的最优策略通常是确定性策略，因为其是从众多行为价值中选择一个 最大价值的行为，而有些问题的最优策略却是随机策略，这种情况下同样是无法通过基于价值的学习来求解的。
  • 这其中最简单的一个例子是人们小时候经常玩的“石头剪刀布”游戏。对于这个 游戏，玩家的最优策略是随机出石头剪刀布中的一个，因为一旦你遵循一个确定的策略，将很容 易被对手发现并利用进而输给对方

定义

• 策略 π 可以被被描述为一个包含参数 θ 的函数
  $π_θ(s,a) = P[a | s,θ]$
• 含义：
  策略函数 $π_θ$ 确定了在给定的状态和一定的参数设置下，采取任何可能行为的概率，是一个概率密度函数
  • 在实际应用这个策略时，选择最大概率对应的行为或者以此为基础进行一定程度的采样探索。可以认为，参数 θ 决定了策略的具体形式。
  • 因而求解基于策略的学习问题就转变为了如何确定策略函数的参数 θ。同样可以通过设计一个基于参数 θ 的目标函数 J(θ)，通过相应 的算法来寻找最优参数

策略目标函数

强化学习的目标就是让个体在与环境交互过程中获得尽可能多的累计奖励，一个好的策略 应该能准确反映强化学习的目标

• 初始状态收获的期望
  对于一个能够形成完整状态序列的交互环境来说，由于一个策 略决定了个体与环境的交互，因而可以设计目标函数 J1(θ) 为使用策略 πθ 时初始状态价值 (start value):
  $J_1(θ) = V_{π_θ} (s_1) = E_{π_θ} [G_1]$
• 有些环境是没有明确的起始状态和终止状态，个体持续的与环境进行交互。在这种情况下可以使 用平均价值 (average value) 或者每一时间步的平均奖励 (average reward per time-step) 来设计策
  略目标函数:
  • $d^{πθ} (s)$ 是基于策略 $πθ$生成的马尔科夫链关于状态的静态分布
• 与价值函数近似的目标函数 不同，策略目标函数的值越大代表着策略越优秀。可以使用与梯度下降相反的梯度上升来求解最优参数
• 假设现在有一个单步马尔科夫决策过程，对应的强化学习问题是个体与环境每产生一个行 为交互一次即得到一个即时奖励 r = Rs,a，并形成一个完整的状态序列。根据公式 (7.1)，策略目 标函数为
• 分值函数(score function)
  上式中 $∇θlogπθ(s,a)$ 称为分值函数 (score function)。
  • 存在如下的策略梯度定理:
    对于任何 可微的策略函数 $π_θ(s, a)$ 以及三种策略目标函数 $J = J_1, J_{avV} 和 J_{avR}$ 中的任意一种来说，策略 目标函数的梯度 (策略梯度) 都可以写成用分值函数表示的形式:
  • 意义
    • 分值越高意味着在当前策略下对应行为被选中的概率越大
    • 算法将结合某一行为的分值对应的奖励来得到对应的梯度，并在此基础上调整参 数，最终使得奖励越大的行为对应的分值越高

Actor-Critic 算法

定义

• Actor-Critic 算法的名字很形象，它包含一个策略函数和行为价值函数
  • 其中策略函数充当 演员 (Actor), 生成行为与环境交互
  • 行为价值函数充当 (Critic)，负责评价演员的表现，并指导 演员的后续行为动作
• Critic 的行为价值函数是基于策略 $π_θ$ 的一个近似
  $Q_w(s, a) ≈ Q_{π_θ} (s, a)$
• 基于此，Actor-Critic 算法遵循一个近似的策略梯度进行学习

QAC算法(最基本的基于行为价值 Q 的 Actor-Critic 算法)

参数更新

• Critic 的函数 $V_w(s)$ 的参数 w更新
• 策略函数 $π_θ(s,a)$ 的参数θ更新

深度确定性策略梯度(DDPG)算法

DDPG算法能较为稳定地解决连续行为空间下强化学习问题

算法理解

• 深度确定性策略梯度算法是使用深度学习技术、同时基于 Actor-Critic 算法的确定性策略算法
• 该算法中的 Actor 和 Critic 都使用深度神经网络来建立近似函数
• 由于该算法可以直接从 Actor 的策略生成确定的行为而不需要依据行为的概率分布进行采样而被称为确定性策略
• 噪声函数
  该算法在学习阶段通过在确定性的行为基础上增加一个噪声函数而实现在确定性行为周围的小范围 内探索
• 备份了一套参数
  • 该算法还为 Actor 和 Critic 网络各备份了一套参数用来计算行为价值的期待值以更稳定地提升 Critic 的策略指导水平。使用备份参数的网络称为目标网络，其对应的参数每次更新的幅度很小
  • 另一套参数对应的 Actor 和 Critic 则用来生成实际交互的行为以及计算相应 的策略梯度，这一套参数每学习一次就更新一次。这种双参数设置的目的是为了减少因近似数据 的引导而发生不收敛的情形。
• 这四个网络具体使用的情景为
  • Actor 网络:根据当前状态 $s_0$ 生成的探索或不探索的具体行为$a_0$;
  • Target Actor 网络:根据环境给出的后续状态$s_1$ 生成预估价值用到的$a_1$;
  • Critic 网络:计算状态$s_0$和生成的行为$a_0$ 对应的行为价值;
  • Target Critic 网络:根据后续状态$ s_1,a_1 生成用来计算目标价值 y = Q(s_0, a_0) 的 Q′(s_1, a_1)$

伪代码

背景

• 问题的复杂性

  • 本章之前的内容介绍的多是规模比较小的强化学习问题，生活中有许多实际问题要复杂得 多，有些是属于状态数量巨大甚至是连续的，有些行为数量较大或者是连续的。这些问题要是使 用前几章介绍的基本算法效率会很低，甚至会无法得到较好的解决
  • 解决这类问题的常用方法是不再使用字典之类的查表式的方法来存储状态或行为的价值，而 是引入适当的参数，选取恰当的描述状态的特征，通过构建一定的函数来近似计算得到状态或行 为价值
  • 在引入近似价值函数后，强化学习中不管是预测问题还是控制问题，就转变成近似函数的设 计以及求解近似函数参数这两个问题了

• 状态价值 $v_π(s)$ 的近似表示
  如果能建立一个函数 vˆ, 这个函数由参数 w 描述，它可以直接接受表示状态特征的连续变量 s 作为输入，通过计算得到一个状态的价值，通过调整参数 w 的取值，使得其符合基于某一策略 π 的最终状态价值，那么这个函数就是状态价值 $v_π(s)$ 的近似表示
  $\hat v{(s,w)} ≈ v_π(s)$

• 行为价值 $q_π(s,a)$ 的近似表示
  $\hat q(s,a,w) ≈ q_π(s,a)$

  

常用的近似价值函数(DQN算法)

理论上任何函数都可以被用作近似价值函数，实际选择何种近似函数需根据问题的特点。比较常用的近似函数有线性函数组合、神经网络、决策树、傅里叶变换等等,这里会重点介绍基于深度学习的神经网络计数进行特征表示，包括卷积神经网络。

DQN算法

DQN 算法主要使用经历回放 (experience replay) 来 实现价值函数的收敛。其具体做法为:

• 个体能记住既往的状态转换经历，对于每一个完整状态序 列里的每一次状态转换，
• 依据当前状态的 $st 价值以 ε-贪婪策略选择一个行为 a_t，执行该行为得 到奖励 r_{t+1} 和下一个状态 s_{t+1}$
• 将得到的状态转换存储至记忆中
• 当记忆中存储的容量足够大时，随机从记忆力提取一定数量的状态转换
• 用状态转换中下一状态来计算当前状态的目标价值，使用公式 (6.4) 计算目标价值与网络输出价值之间的均方差代价，使用小块梯度下降算法更 新网络的参数

• 伪代码
  • 该算法中 的状态 S 都由特征 φ(S) 来表示

DDQN(double deep Q network)

• 背景：
  DQN得了不俗的成绩，不过其并不能保证一直收敛，研究表明这种估计目标价值的算法过于乐观的高 估了一些情况下的行为价值，导致算法会将次优行为价值一致认为最优行为价值，最终不能收敛 至最佳价值函数
• 和DQN区别
  该算法使用两个架构相同的近似价值函数：
  • 其中一个用来根据策略生成交互行为并随 时频繁参数 (θ)
  • 另一个则用来生成目标价值, 其参数 (θ−) 每隔一定的周期进行更新。该算法绝 大多数流程与 DQN 算法一样，只是在更新目标价值时使用公式 (6.20):
  • 该式表明，DDQN 在生成目标价值时使用了生成交互行为并频繁更新参数的价值网络 Q(θ)， 在这个价值网络中挑选状态 S′下最大价值对应的行为 $A′_t$，随后再用状态行为对 $(S_t′, A′_t)$ 代入目标价值网络 Q(θ−) 得出目标价值。实验表明这样的更改比 DQN 算法更加稳定，更容易收敛值 最优价值函数和最优策略
• 同样存在深度学习的问题
  在使用神经网络等深度学习技术来进行价值函数近似时，有可能会碰到无法得到预期结果的情况,深度学习的问题这里也会遇到

背景

本章内容

• 前一章内容讲解了个体在不依赖模型的情况下如何进行预测，也就是求解在给定策略下的 状态价值或行为价值函数
• 本章则主要讲解在不基于模型的条件下如何通过个体的学习优化价值函数，同时改善自身行为的策略以最大化获得累积奖励的过程，这一过程也称作不基于模型的 控制

问题举例

• 生活中有很多关于优化控制的问题，比如控制一个大厦内的多个电梯使得效率最高;
• 控制直 升机的特技飞行
• 机器人足球世界杯上控制机器人球员，围棋游戏等等
• 两类问题：
  • 所有的这些问题要么我们对其环境动力学的特点无法掌握，但是我们可以去经历、去尝试构建理解环境的模型;
  • 要么虽然问题的环境动力学特征是已知的，但由问题的规模太大以至于计算机根据一般算法无法高效 的求解，除非使用采样的办法。
  • 无论问题是属于两种情况中的哪一个，强化学习都能较好的解决

相关概念

• 行为策略
  我们把用来指导个体产生与环境进 行实际交互行为的策略称为行为策略
• 目标策略(优化策略)
  把用来评价状态或行为价值的策略或者待优化的策略称 为目标策略。
• 现时策略学习 (on-policy learning)
  个体在学习过程中优化的策略与自己的行为策略是同一个策略时，这种学习方 式称为现时策略学习 (on-policy learning)
• 借鉴策略学习 (off-policy learning)
  个体在学习过程中优化的策略与自己的行为策略 是不同的策略时，这种学习方式称为借鉴策略学习 (off-policy learning)

算法的整体关系

• 从已知模型的、基于全宽度采样的动态规划学习转至模型未知的、基于采样的蒙特卡洛或时序差分学习进行控制是朝着高效解决中等规模实际问题的一个突破
• 基于这些思想产生了一 些经典的理论和算法:
  • 如不完全贪婪搜索策略、现时蒙特卡洛控制，现时时序差分学习
  • 属于借鉴学习算法的 Q 学习等

行为价值函数的重要性

• 生活学习哲学到强化学习
  • 生活中有些人喜欢做事但不善于总结，这类人一般要比那些勤于总结的人进步得慢，从策略 迭代的角度看，
    • 这类人策略更新迭代的周期较长
    • 有些人在总结经验上过于勤快，甚至在一件事 情还没有完全定论时就急于总结并推理过程之间的关系，这种总结得到的经验有可能是错误的
  • 强化学习中的个体也是如此，为了让个体的尽早地找到最优策略，可以适当加快策略迭代的速 度:
    • 但是从一个不完整的状态序列学习则要注意不能过多地依赖状态序列中相邻状态行为对的 关系。
    • 由于基于蒙特卡洛的学习利用的是完整的状态序列，为了加快学习速度可以在只经历一个完整状态序列后就进行策略迭代
    • 而在进行基于时序差分的学习时，虽然学习速度可以更快，但 要注意减少对事件估计的偏差

ε− 贪婪策略

背景

• 如上在动态规划策略迭代中，可看见：贪婪搜索策略在基于模型的动态规划算法中能收敛至最优 策略(价值)，但这在不基于模型、基于采样的蒙特卡罗或时序差分学习中却通常不能收敛至最优策略
• 因为后两者则仅能考虑到有限次数的、已经采样经历过 的状态，那些事实存在但还没经历过的状态对于后两者算法来说都是未探索的不被考虑的状态
  • 有些状态虽然经历过，但由于经历次数不多对其价值的估计也不一定准确。
  • 如果存在一些价值更高的未被探索的状态使用贪婪算法将式中无法探索到这些状态，而已经经历过但价值较低的状 态也很难再次被经历，如此将无法得到最优策略
• 总体来说，使用贪婪策略，在MC,TD中，因为是采样，会导致有些状态不能经历或者经历的次数不够，造成无法得到最优策略
• 贪婪策略产生问题的根源是无法保证持续的探索，为了解决这个问题，一种不完全的贪婪 (ε-greedy 搜索策略被提出，其基本思想就是保证能做到持续的探索，具体通过设置一个较小的 ε 值，使用 1 − ε 的概率贪婪地选择目前认为是最大行为价值的行为，而用 ε 的概率随机的从所有m 个可选行为中选择行为，即:

现时策略蒙特卡罗控制

定义

现时策略蒙特卡罗控制通过 ε-贪婪策略采样一个或多个完整的状态序列后，平均得出某一状态行为对的价值，并持续进行策略的评估和改善。通常可以在仅得到一个完整状态序列后就进行一次策略迭代以加速迭代过程

GLIE

• 背景
  使用 ε-贪婪策略进行现时蒙特卡罗控制仍然只能得到基于该策略的近似行为价值函数，这 是因为该策略一直在进行探索，没有一个终止条件。因此我们必须关注以下两个方面:

  • 一方面我 们不想丢掉任何更好信息和状态
  • 另一方面随着我们策略的改善我们最终希望能终止于某一个最优策略

  为此引入了另一个理论概念:GLIE(greedy in the Limit with Infinite Exploration)

• 含义

  • 一是所有的状态行为对会被无限次探索
  • 二是另外随着采样趋向无穷多，策略收敛至一个贪婪策略:
  • 定理：GLIE 蒙特卡洛控制能收敛至最优的状态行为价值函数

GLIE应用

如果在使用 ε-贪婪策略时，能令 ε 随采样次数的无限增加而趋向于 0 就符合 GLIE。这样基 于 GLIE 的蒙特卡洛控制流程如下:

• 基于给定策略 π，采样第 k 个完整的状态序列:${S_1, A_1, R_2, · · · , S_T}$
• 对于该状态序列里出现的每一状态行为对$(S_t, A_t)$，更新其计数N 和行为价值函数Q:
• 基于新的行为价值函数 Q 以如下方式改善策略
  • 在实际应用中，ε 的取值可不局限于取 1/k，只要符合 GLIE 特性的设计均可以收敛至最优策略(价值)

现时策略时序差分控制

前言介绍

• 预测问题上TD比MC有点多
  我们体会到时序差分 (TD) 学习相比蒙特卡罗 (MC) 学习有很 多优点:低变异性，可以在线实时学习，可以学习不完整状态序列等
• 控制问题上任很多优点,会介绍一些算法
  在控制问题上使用TD学习同样具备上述的一些优点。
  • 本节的现时策略TD学习中，我们将介绍Sarsa算法和Sarsa(λ)算法
  • 在下一节的借鉴策略TD学习中将详细介绍Q学习算法

Sarsa 算法

• 算法理解
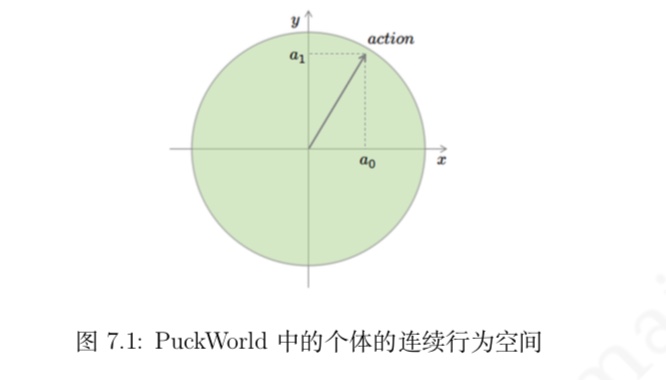
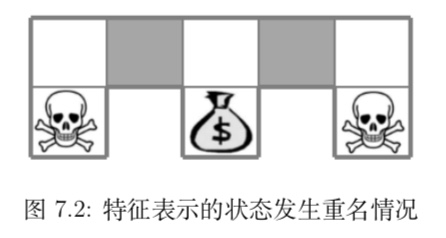
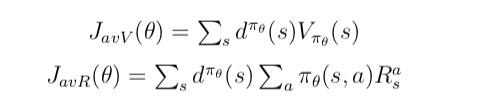
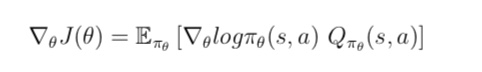
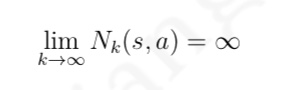
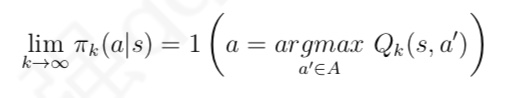
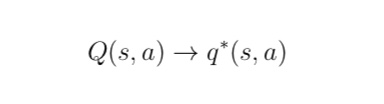
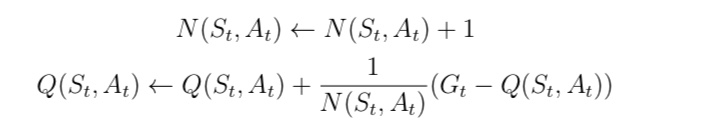
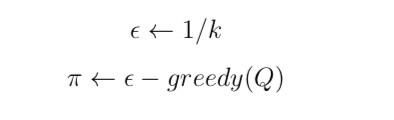
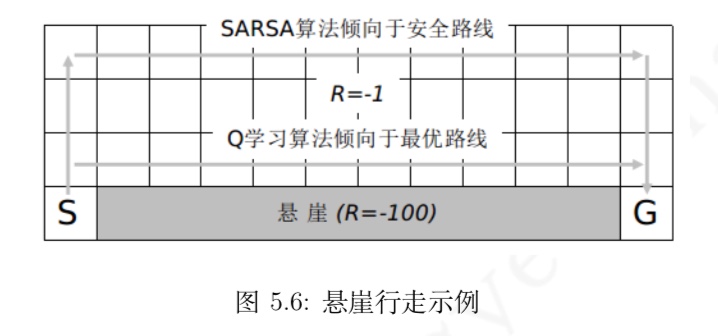
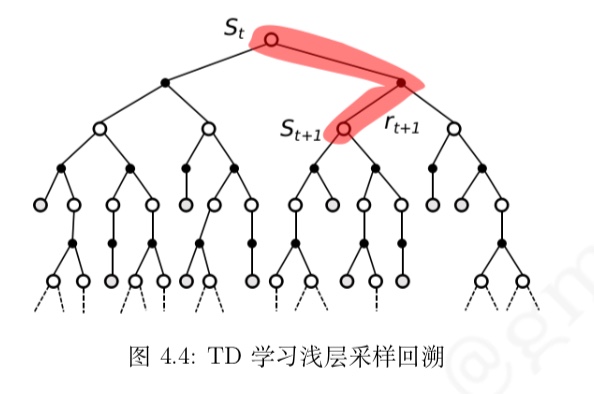
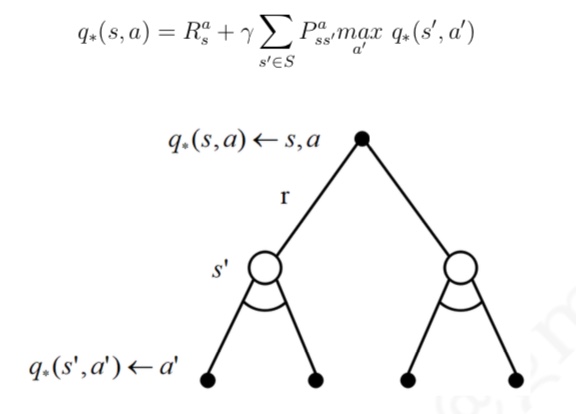
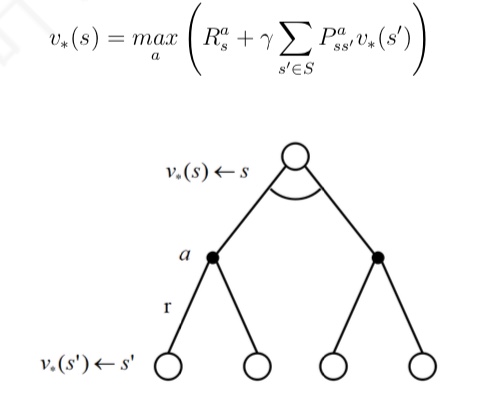
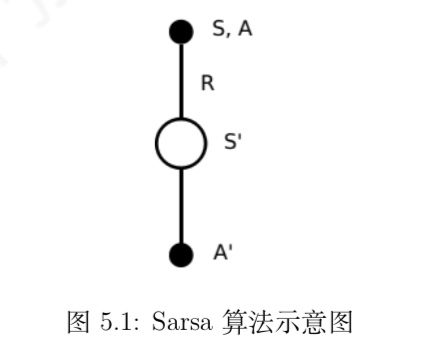  Sarsa 的名称来源于下图所示的序列描述:针对一个状态 S，个体通过行为策略产生一个行 为 A，执行该行为进而产生一个状态行为对 (S,A)，环境收到个体的行为后会告诉个体即时奖励 R 以及后续进入的状态 S’;个体在状态 S’ 时遵循当前的行为策略产生一个新行为 A’，个体此时 并不执行该行为，而是通过行为价值函数得到后一个状态行为对 (S’,A’) 的价值，利用这个新的 价值和即时奖励 R 来更新前一个状态行为对 (S,A) 的价值 与 MC 算法不同的是，Sarsa 算法在单个状态序列内的每一个时间步，在状态 S 下采取一个 行为 A 到达状态 S’ 后都要更新状态行为对 (S,A) 的价值 Q(S,A)。这一过程同样使用 ε-贪婪策略进行策略迭代:
• 算法伪代码
• Sarsa 算法将收敛至最优策略和最优价值函数条件
  • 在更新行为价值时，参数 α 是学习速率参数，γ 是衰减因子。当行为策略满足前文所述的 GLIE 特性同时学习速率参数 α 满足
• 举例：有风格子
  • 为了使用计算机程序解决这个问题，我们首先将这个问题用强化学习的语言再描述一遍。这是一个不基于模型的控制问题，也就是要在不掌握马尔科夫决策过程的情况下寻找最优策略。环 境世界中每一个格子可以用水平和垂直坐标来描述，如此构成拥有 70 个状态的状态空间 S。行 为空间 A 具有四个基本行为。环境的的动力学特征不被个体掌握，但个体每执行一个行为，会进入一个新的状态，该状态由环境告知个体，但环境不会直接告诉个体该状态的坐标位置。即时 奖励是根据任务目标来设定，现要求尽快从起始位置移动到目标位置，我们可以设定每移动一步 只要不是进入目标位置都给予一个 -1 的惩罚，直至进入目标位置后获得奖励 0 同时永久停留在 该位置
  • 这里先给出最 优策略为依次采取如下的行为序列:
    右、右、右、右、右、右、右、右、右、下、下、下、下、左、左
    个体找到该最优策略的进度以及最优策略下个体从起始状态到目标状态的行为轨迹如图 5.3 所示。
  • 可以看出个体在一开始的几百甚至上千步都在尝试各种操作而没有完成一次从起始位置到 目标位置的经历。不过一旦个体找到一次目标位置后，它的学习过程将明显加速，最终找到了一 条只需要 15 步的最短路径。由于世界的构造以及其内部风的影响，个体两次利用风的影响，先向右并北漂到达最右上角后折返南下再左移才找到这条最短路径。其它路径均比该路径所花费
    的步数要多

Sarsa(λ)算法

可以结合TD(λ)对比理解,这里不做详细介绍

• 在前一章，我们学习了 n-步收获，这里类似的引出一个 n-步 Sarsa 的概念。观察下面一些列的式子

借鉴策略Q学习算法

背景

现时策略学习的特点就是产生实际行为的策略与更新价值 (评价) 所使用的策略是同一个策 略，而借鉴策略学习 (off-policy learning) 中产生指导自身行为的策略 μ(a|s) 与评价策略 π(a|s) 是不同的策略

• 具体地说，个体通过策略 μ(a|s)生成行为与环境发生实际交互，但是在更新这个状态行为对的价值时使用的是目标策略 π(a|s)
• 目标策略 π(a|s) 多数是已经具备一定能力的 策略，例如人类已有的经验或其他个体学习到的经验

借鉴策略学习相当于站在目标策略 π(a|s)的“肩膀”上学习。

• 借鉴策略学习根据是否经历完整的状态序列可以将其分为基于蒙特卡洛的和 基于 TD 的。
  • 基于蒙特卡洛的借鉴策略学习目前认为仅有理论上的研究价值，在实际中用处不 大。
  • 这里主要讲解常用借鉴策略 TD 学习

借鉴学习TD学习任务

• 借鉴学习 TD 学习任务就是使用 TD 方法在目标策略 π(a|s) 的基础上更新行为价值，进而优化行为策略
• 我们可以这样理解:个体处在状态 $S_t$ 中，基于行为策略 μ 产生了一个行为 $A_t$， 执行该行为后进入新的状态 $S_{t+1}$，借鉴策略学习要做的事情就是，比较借鉴策略和行为策略在状 态 $S_t$ 下产生同样的行为 $A_t$ 的概率的比值(其实就是看此次对该状态价值的更新支持程度):
  • 如果这个比值接近 1，说明两个策略在状态 $S_t$ 下采 取的行为 $A_t$ 的概率差不多，此次对于状态 $S_t$ 价值的更新同时得到两个策略的支持
  • 如果这一概率比值很小，则表明借鉴策略 π 在状态 $S_t$ 下选择 $A_t$ 的机会要小一些，此时为了从借鉴策略 学习，我们认为这一步状态价值的更新不是很符合借鉴策略，因而在更新时打些折扣。
  • 如果这个概率比值大于 1，说明按照借鉴策略，选择行为 $A_t$ 的几率要大于当前行为策略产生 $A_t$的概率，此时应该对该状态的价值更新就可以大胆些

Q学习

• 借鉴学习TD学习任务的典型分支

  • 行为策略 μ 是基于行为价值函数 Q(s, a) ε-贪婪策略
  • 借鉴 策略 π 则是基于 Q(s, a) 的完全贪婪策略

  这种学习方法称为 Q 学习 (Q learning)

• Q学习的目标
  Q 学习的目标是得到最优价值 Q(s,a)
• 策略μ
  t 时刻的与环境进行实际交互 的行为$A_t$由策略μ产生:$A_t ∼ μ(·|S_t)$,其中策略 μ 是一个 ε-贪婪策略
• 策略π
  t + 1 时刻用来更新 Q 值的行为 $A’{t+1}$ 由下式产生:$ A’{t+1} ∼ π(·|S_{t+1}) $。其中策略 π 是一个完全贪婪策略

• $Q(S_t, A_t)$ 的按下式更新

  
  • 其中红色部分的 TD 目标是基于借鉴策略 π 产生的行为 A’ 得到的 Q 值。
  • 根据这种价值更 新的方式
    • 状态 $S_t$ 依据 ε-贪婪策略得到的行为 $A_t$ 的价值将朝着 $S_{t+1}$ 状态下贪婪策略确定的最 大行为价值的方向做一定比例的更新
    • 这种算法能够使个体的行为策略策略 μ 更加接近贪婪策 略，同时保证保证个体能持续探索并经历足够丰富的新状态。

  并最终收敛至最优策略和最优行为价值

  
  • 下图是 Q 学习具体的行为价值更新公式
    • 注意和上式比较max部分就是基于贪婪策略得到
• 伪代码

Q学习和Sarsa比较

这里通过悬崖行走的例子 (图) 简要讲解 Sarsa 算法与 Q 学习算法在学习过程中的差别。任 务要求个体从悬崖的一端以尽可能快的速度行走到悬崖的另一端，每多走一步给以 -1 的奖励。 图中悬崖用灰色的长方形表示，在其两端一个是起点，一个是目标终点。个体如果坠入悬崖将得 到一个非常大的负向奖励 (-100) 回到起点。可以看出最优路线是贴着悬崖上方行走。Q 学习算 法可以较快的学习到这个最优策略，但是 Sarsa 算法学到的是与悬崖保持一定的距离安全路线。 在两种学习算法中，由于生成行为的策略依然是 ε 贪婪的，因此都会偶尔发生坠入悬崖的情况， 如果 ε 贪婪策略中的 ε 随经历的增加而逐渐趋于 0，则两种算法都将最后收敛至最优策略

背景

• 讲解如何解决一个可以被认为是 MDP、但却不掌握 MDP 具体细节(比如状态转移概率等等)的问题
• 从本章开始的连续两章内容将讲解如何解决一个可以被认为是 MDP、但却不掌握 MDP 具体细节的问题，也就是讲述个体如何在没有对环境动力学认识的模型的条件下如何直接 通过个体与环境的实际交互来评估一个策略的好坏或者寻找到最优价值函数和最优策略。其中 本章将聚焦于策略评估，也就是预测问题

蒙特卡罗强化学习 (Monte-Carlo reinforcement learning)

• MC：
  指在不清楚 MDP 状态 转移概率的情况下，直接从经历完整的状态序列 (episode) 来估计状态的真实价值，并认为某状 态的价值等于在多个状态序列中以该状态算得到的所有收获的平均
• MC特点：
  蒙特卡罗强化学习有如下特点:不依赖状态转移概率，直接从经历过的完整的状态序列中学习，使用的思想就是用平均收获值代替价值。理论上完整的状态序列越多，结果越准确
• 完整的状态序列 (complete episode):
  指从某一个状态开始，个体与环境交互直到终止状态， 环境给出终止状态的奖励为止。
  • 完整的状态序列不要求起始状态一定是某一个特定的状态，但是 要求个体最终进入环境认可的某一个终止状态
• MC含义举例说明:
  • 基于特定策略 π 的一个 Episode 信息可以表示为如下的一个序列:$S_1,A_1,R_2,S_2,A_2,…,S_t,A_t,R_{t+1},…,S_k ∼π$
  • t 时刻状态 St 的收获可以表述为:
    $G_t =R_{t+1} +γR_{t+2} +…+γ(T−1)R_T$
  • 其中 T 为终止时刻。该策略下某一状态 s 的价值:
    $v_π(s) = E_π[G_t|S_t = s]$
• 一个序列中出现多次状态的问题
  • 如果一个完整的状态序列中某一需要计算的状态出现在序列的多个位置， 也就是说个体在与环境交互的过程中从某状态出发后又一次或多次返回过该状态,处理的两种方法：
    • 首次访问:仅把状态序列中第一次出现该状 态时的收获值纳入到收获平均值的计算中
    • 每次访问:针对一个状态序列中每次出现的该状态，都 计算对应的收获值并纳入到收获平均值的计算中
• 求解技巧
  • 累进更新平均值(incremental mean)。而且这种计算平均值的思想也是强化学习的一 个核心思想之一
  • 在求解状态收获的平均值的过程中，我们介绍一种非常实用的不需要存储所有历史收获的 计算方法:累进更新平均值(incremental mean)
  • 如果把该式中平均值和新数据分别看成是状态的价值和该状态的收获，那么该公式就变成了递增式的蒙特卡罗法更新状态价值。其公式如下:

时序差分强化学习

• 定义：
  指从采样得到的 不完整的状态序列学习，该方法通过合理的引导(bootstrapping)，先估计某状态在该状态序列 完整后可能得到的收获，并在此基础上利用前文所属的累进更新平均值的方法得到该状态的价 值，再通过不断的采样来持续更新这个价值
  • 具体地说，在 TD 学习中，算法在估计某一个状态的收获时，用的是离开该状态的即刻奖励 $R_{t+1}$ 与下一时刻状态 $S_{t+1}$ 的预估状态价值乘以衰减系数 γ 组成:
    $V(S_t) ← V(S_t) + α(R_{t+1} + γV(S_{t+1}) − V(S_t))$
    • 其中:$R_{t+1} + γV(S_{t+1}) 称为 TD 目标值。R_{t+1} + γV(S_{t+1}) − V(S_t)$称为 TD 误差
    • 引导 (bootstrapping):指的是用 TD 目标值代替收获 $G_t$ 的过程

MC,TD,DP比较

• MC,TD相同点：
  • 不依赖于模型
  • 它们都不再需要清楚某一状态的所有可能的后
    续状态以及对应的状态转移概率
  • 因此也不再像动态规划算法那样进行全宽度的回溯来更新状 态的价值。
  • MC 和 TD 学习使用的都是通过个体与环境实际交互生成的一系列状态序列来更新 状态的价值。这在解决大规模问题或者不清楚环境动力学特征的问题时十分有效
• DP 算法则是基于模型的计算状态价值的方法，它通过计算一个状态 S 所 有可能的转移状态 S’ 及其转移概率以及对应的即时奖励来计算这个状态 S 的价值
• 是否使用引导数据：
  • MC 学习并不使用引导数据，它使用实际产生的奖励值来计算状态 价值
  • TD 和 DP 则都是用后续状态的预估价值作为引导数据来计算当前状态的价值
• 是否采样：
  • MC 和 TD 不依赖模型，使用的都是个体与环境实际交互产生的采样 状态序列来计算状态价值的
  • DP 则依赖状态转移概率矩阵和奖励函数，全宽度计算状态价 值，没有采样之说。
• MC算法
  深度采样学习。一次学习完整经历，使用实际收获更新状态预估价值
• TD 算法:
  浅层采样学习。经历可不完整，使用后续状态的预估状态价值预估收获再更新当前状态价值
• DP算法：
  浅层全宽度 (采样) 学习。依据模型，全宽度地使用后续状态预估价值来更新当前
  状态价值
• 小结：
  • 当使用单个采样，同时不经历完整的状态序 列更新价值的算法是 TD 学习;
  • 当使用单个采样，但依赖完整状态序列的算法是 MC 学习;
  • 当考虑全宽度采样，但对每一个采样经历只考虑后续一个状态时的算法是 DP 学习;
  • 如果既考虑所 有状态转移的可能性，同时又依赖完整状态序列的，那么这种算法是穷举 (exhausive search) 法。
  • 需要说明的是:DP 利用的是整个 MDP 问题的模型，也就是状态转移概率，虽然它并不实际利 用采样经历，但它利用了整个模型的规律，因此也被认为是全宽度 (full width) 采样的

n步时序差分学习简介

定义

• 第二节所介绍的 TD 算法实际上都是 TD(0) 算法，括号内的数字 0 表示的是在当前状态下 往前多看 1 步

λ-收获

为了能在不增加计算复杂度的情况下综合考虑所有步数的预测，我们引入了一个新的参数 λ，并定义:λ-收获

• 任意一个 n-步收获的权重被设计为 $(1 − λ)λ^{n−1}$，如图 4.7 所示。通过这样的权重设计，可以得到 λ-收获的计算公式为
• 对应的 TD(λ) 被描述为

背景

动态规划理解

• 规划
  “规划”是在已知环 境动力学的基础上进行评估和控制，具体来说就是在了解包括状态和行为空间、转移概率矩阵、 奖励等信息的基础上判断一个给定策略的价值函数，或判断一个策略的优劣并最终找到最优的 策略和最优价值函数

• 动态规划算法把求解复杂问题分解为求解子问题，通过求解子问题进而得到整个问题的解,在解决子问题的时候，其结果通常需要存储起来被用来解决后续复杂问题

  • 当问题具有下列两个 性质时，通常可以考虑使用动态规划来求解:
    • 第一个性质是一个复杂问题的最优解由数个小问题 的最优解构成，可以通过寻找子问题的最优解来得到复杂问题的最优解;
    • 第二个性质是子问题在 复杂问题内重复出现，使得子问题的解可以被存储起来重复利用

• 和马尔科夫决策过程关系
  马尔科夫决策过程具有上述两 个属性:

  • 贝尔曼方程把问题递归为求解子问题
  • 价值函数相当于存储了一些子问题的解，可以复 用。因此可以使用动态规划来求解马尔科夫决策过程

预测和控制

• 预测 (prediction):已知一个马尔科夫决策过程 MDP ⟨S, A, P, R, γ⟩ 和一个策略 π，或者是 给定一个马尔科夫奖励过程 $MRP ⟨S, P_π, R_π, γ⟩$，求解基于该策略的价值函数 $v_π$。
• 控制(control):已知一个马尔科夫决策过程MDP⟨S,A,P,R,γ⟩，求解最优价值函数v∗ 和 最优策略 π∗。

策略评估

含义

指计算给定策略下状态价值函数的过程
对策略评估，我们可 以使用同步迭代联合动态规划的算法:从任意一个状态价值函数开始，依据给定的策略，结合贝 尔曼期望方程、状态转移概率和奖励同步迭代更新状态价值函数，直至其收敛，得到该策略下最 终的状态价值函数

• 贝尔曼期望方程给出了如何根据状态转换关系中的后续状态 s′ 来计算当前状态 s 的价值， 在同步迭代法中，我们使用上一个迭代周期 k 内的后续状态价值来计算更新当前迭代周期 k + 1
  内某状态 s 的价值
  • 我们可以对计算得到的新的状态价值函数再次进行迭代，直至状态函数收敛，也就是迭代计算得到每一个状态的新价值与原价值差别在一个很小的可接受范围内

举例(小型方格世界迭代中的价值函数)

• 均一概率的随机策略

策略迭代

背景

完成对一个策略的评估，将得到基于该策略下每一个状态的价值。很明显，不同状态对应的 价值一般也不同，那么个体是否可以根据得到的价值状态来调整自己的行动策略呢

迭代过程理解(贪婪策略)

个体在某个状态下选择的行为是其能够到达后续所有可能的状态中价值最 大的那个状态。我们以均一随机策略下第 2 次迭代后产生的价值函数为例说明这个贪婪策略

• 新的贪婪策略比之前的均一随机策略要优秀不少，至少在靠近终止
  状态的几个状态中，个体将有一个明确的行为，而不再是随机行为了。我们从均一随机策略下的 价值函数中产生了新的更优秀的策略，这是一个策略改善的过程

• 我的理解：
  上面左图是各个状态的价值，右图是各个状态的策略，选择的贪婪策略由于各个状态不同的价值，导致了右图不同的策略。然后又由于不同的策略，执行下一步行动，继续会导致左图中不同的状态，以此循环

  • 依据新的策略 π′ 会得到一个新的价值函数，并产生新的贪婪策略，如此重复循环迭代将最 终得到最优价值函数 v∗ 和最优策略 π∗

• 策略迭代

  • 策略在循环迭代中得到更新改善的过程称为策略迭代
  • 从一个初始策略 π 和初始价值函数 V 开始，基于该策略进行完整的价值评估过程得到一个 新的价值函数，随后依据新的价值函数得到新的贪婪策略，随后计算新的贪婪策略下的价值函 数，整个过程反复进行，在这个循环过程中策略和价值函数均得到迭代更新，并最终收敛值最有 价值函数和最优策略

价值迭代

背景

细心的读者可能会发现，如果按照图 3.2 中第三次迭代得到的价值函数采用贪婪选择策略的 话，该策略和最终的最优价值函数对应的贪婪选择策略是一样的，它们都对应于最优策略，如图 3.5，而通过基于均一随机策略的迭代法价值评估要经过数十次迭代才算收敛。这会引出一个问 题:是否可以提前设置一个迭代终点来减少迭代次数而不影响得到最优策略呢?是否可以每迭代 一次就进行一次策略评估呢

最优策略的意义

• 任何一个最优策略可以分为两个阶段:
  首先该策略要能产生当前状态下的最优行为，其次对 于该最优行为到达的后续状态时该策略仍然是一个最优策略

• 直观感受(单纯的价值迭代)

  

  这个公式带给我们的直觉是如果我们能知道最终状态的价值和相关奖励，可以直接计算得 到最终状态的前一个所有可能状态的最优价值。更乐观的是，即使不知道最终状态是哪一个状 态，也可以利用上述公式进行纯粹的价值迭代，不停的更新状态价值，最终得到最优价值，而且 这种单纯价值迭代的方法甚至可以允许存在循环的状态转换乃至一些随机的状态转换过程

举例

• 首先考虑到个体知道环境的动力学特征的情形。在这种情况下，个体可以直接计算得到与终 止状态直接相邻(斜向不算)的左上角两个状态的最优价值均为 −1。随后个体又可以往右下角 延伸计算得到与之前最优价值为 −1 的两个状态香相邻的 3 个状态的最优价值为 −2。以此类推， 每一次迭代个体将从左上角朝着右下角方向依次直接计算得到一排斜向方格的最优价值，直至 完成最右下角的一个方格最优价值的计算
• 个人理解：
  由于上面的直观感受可以知道，前一状态的最优价值可以由后一状态计算得到，所以从最终的终态出发，开始价值为0，然后倒推，得到每一个状态的最优价值（纯粹的价值迭代，并没有策略的参与）
• 特点(注意并没有策略的参与)
  价值迭代的目标仍然是寻找到一个最优策略，它通过贝尔曼最优方程从前次迭代 的价值函数中计算得到当次迭代的价值函数，在这个反复迭代的过程中，并没有一个明确的策略 参与
  • 需要 注意的是，在纯粹的价值迭代寻找最优策略的过程中，迭代过程中产生的状态价值函数不一定对 应一个策略。迭代过程中价值函数更新的公式为:

同步动态规划算法总结

使用同步动态规划进行规划基本就讲解完毕了。前文所述的这三类算法均是基于状态价值函数的

• 其中迭代法策略评估属于预测问题，它使用贝尔曼期望方程来进行求解。
• 策略迭代和价值迭代则属于控制问题
  • 其中前者使用贝尔曼 期望方程进行一定次数的价值迭代更新，随后在产生的价值函数基础上采取贪婪选择的策略改 善方法形成新的策略，如此交替迭代不断的优化策略;
  • 价值迭代则不依赖任何策略，它使用贝尔 曼最优方程直接对价值函数进行迭代更新

异步动态规划算法

前文所述的系列算法均为同步动态规划算法，它表示所有的状态更新是同步的。与之对应的 还有异步动态规划算法。在这些算法中，每一次迭代并不对所有状态的价值进行更新，而是依据 一定的原则有选择性的更新部分状态的价值

• 这种算法能显著的节约计算资源，并且只要所有状 态能够得到持续的被访问更新，那么也能确保算法收敛至最优解。
• 比较常用的异步动态规划思想 有:原位动态规划、优先级动态规划、和实时动态规划

背景

• 求解强化学习问题可以理解为如何最大化个体在与环境交互过程中获得的累积奖励
• 当环境状态是完全可观测时，个体可以通过构建马尔科夫决策过程来描述整 个强化学习问题。有时候环境状态并不是完全可观测的，此时个体可以结合自身对于环境的历史 观测数据来构建一个近似的完全可观测环境的描述
  • 从这个角度来说，几乎所有的强化学习问题 都可以被认为或可以被转化为马尔科夫决策过程

马尔科夫过程

马尔科夫性

在一个时序过程中，如果 t + 1 时刻的状态仅取决于 t 时刻的状态 $S_t$ 而与 t 时刻之前的任 何状态都无关时，则认为 t 时刻的状态$S_t$ 具有马尔科夫性 (Markov property)

马尔科夫过程(马尔科夫链)

若过程中的每一 个状态都具有马尔科夫性，则这个过程具备马尔科夫性。具备了马尔科夫性的随机过程称为马尔 科夫过程 (Markov process)，又称马尔科夫链 (Markov chain)

• 描述一个马尔科夫过程的核心是状态转移概率矩阵
  $P_{ss′} = P [S_{t+1} = s′|S_t = s]$
• 通常使用一个元组 ⟨S, P ⟩ 来描述马尔科夫过程，其中 S 是有限数量的状态集，P 是状态转 移概率矩阵

采样

从符合马尔科夫过程给定的状态转移概率矩阵生成一个状态序列的过程称为采样(sample)。

状态序列

采样将得到一系列的状态转换过程，本书我们称为状态序列 (episode)

完整状态序列

当状态序列的最后一个,状态是终止状态时，该状态序列称为完整的状态序列 (complete episode)

马尔科夫奖励过程

背景

马尔科夫过程只涉及到状态之间的转移概率，并未触及强化学习问题中伴随着状态转换的 奖励反馈。如果把奖励考虑进马尔科夫过程，则成为马尔科夫奖励过程(Markov reward process, MRP)。它是由 ⟨S, P, R, γ⟩ 构成的一个元组，其中:

• S 是一个有限状态集
• P 是集合中状态转移概率矩阵:$P_{ss′} = P [S_{t+1} = s′|S_t = s]]$
• R 是一个奖励函数:$R_s = E [R_{t+1}|S_t = s]$
• γ 是一个衰减因子:γ ∈ [0, 1]

相关概念

• 收获
  收获(return)是一个马尔科夫奖励过程中从某一个状态 $S_t$ 开始采样直到终止状态时所有 奖励的有衰减的之和。数学表达式如下
• 价值
  价值(value) 是马尔科夫奖励过程中状态收获的期望。ta 数学表达式为
  $v(s) = E [G_t|S_t = s]$

• 价值函数
  如果存在一个函数，给定一个状态能得到该状态对应的价值，那么该函数就被称为价值函数 (value function)。价值函数建立了从状态到价值的映射

  

• 马尔科夫奖励过程中的贝尔曼方程

  • 它(上图)提示一个状态的价值 由该状态的奖励以及后续状态价值按概率分布求和按一定的衰减比例联合组成
  • 根据马尔科夫奖励过程的定义，$R_{t+1}$ 的期望就是其自身，因为每次离开同一个状 态得到的奖励都是一个固定的值。而下一时刻状态价值的期望，可以根据下一时刻状态的概率分 布得到。如果用 s′ 表示 s 状态下一时刻任一可能的状态:

马尔科夫决策过程(MDP)

背景

马尔科夫奖励过程并不能直接用来指导解决强化学习问题，因为它不涉及到个体行为的选 择，因此有必要引入马尔科夫决策过程。马尔科夫决策过程(Markov decision process, MDP)是 由 ⟨S, A, P, R, γ⟩ 构成的一个元组，其中:

• S 是一个有限状态集
• A 是一个有限行为集
• P 是集合中基于行为的状态转移概率矩阵:$P^a_{ss’} = E [R_{t+1} |S_t = s, A_t = a]$
• R 是基于状态和行为的奖励函数:$R_s^a = E [R_{t+1}|S_t = s, A_t = a]$
• γ 是一个衰减因子:γ ∈ [0, 1]

相关概念

• 策略
  个体在给定状 态下从行为集中选择一个行为的依据则称为策略 (policy)，用字母 π 表示。策略 π 是某一状态下基于行为集合的概率分布:
  $π(a|s)=P[A_t =a|S_t =s]$

  • 策略仅通过依靠当前状态就可以产生一个个体的行为，可以说策略 仅与当前状态相关，而与历史状态无关
  • 策略描述的是个体的行 为产生的机制，是不随状态变化而变化的，被认为是静态的

• 随机策略
  随机策略是一个很常用的策略，当个体使用随机策略时，个体在某一状态下选择的行为并不 确定。借助随机策略，个体可以在同一状态下尝试不同的行为

• 当给定一个马尔科夫决策过程:M = ⟨S, A, P, R, γ⟩ 和一个策略 π，那么状态序列 $S_1, S_2$, . . . 是一个符合马尔科夫过程 $⟨S, P_π⟩$ 的采样

• 价值函数
  价值函数 $v_π(s)$ 是在马尔科夫决策过程下基于策略 π 的状态价值函数，表示从状态 s 开始，遵循当前策略 π 时所获得的收获的期望:$v_π(s) = E [G_t|S_t = s]$

• 行为价值函数(状态行为对价值函数)
  一个基于策略 π 的行为价值函数 $q_π(s,a)$，表示在遵循策略 π 时，对当前状态 s 执行某一具体行为 a 所能的到 的收获的期望:$q_π(s,a) = E[G_t|S_t = s,A_t = a]$

• 贝尔曼方程
  同理，可推导出如下两个方程
  $v_π(s) = E [R_{t+1} + γv_π(S_{t+1})|S_t = s]$
  $q_π(s, a) = E [R_{t+1} + γq_π(S_{t+1}, A_{t+1})|S_t = s, A_t = a]$

状态价值和行为价值转换

• 一个状态的价值可以用该状态下所有行为价值来表达:
  $v_\pi(s) = \sum \pi(a|s)q_\pi(s,a) (a\in A)$

  

• 一个行为的价值可以用该行为所能到达的后续状态的价值来表达:

  

• 把上二式组合起来，可以得到下面的结果:

  

最优价值函数

• 背景：
  是否存在一个基于某一策略的价值函数， 在该策略下每一个状态的价值都比其它策略下该状态的价值高?如果存在如何找到这样的价值 函数?这样的价值函数对应的策略又是什么策略?
• 最优状态价值函数
  是所有策略下产生的众多状态价值函数 中的最大者:$v_∗ = max (v_π(s))$
• 最优行为价值函数(optimal action-value function)
  是所有策略下产生的众多行为价 值函数中的最大者:$q_∗(s,a) = max q_π(s,a)$
• 贝尔曼优化方程
  • 最优状态行为价值
    • 也可以由后续状态行为价值函数得到
  • 最优状态价值：