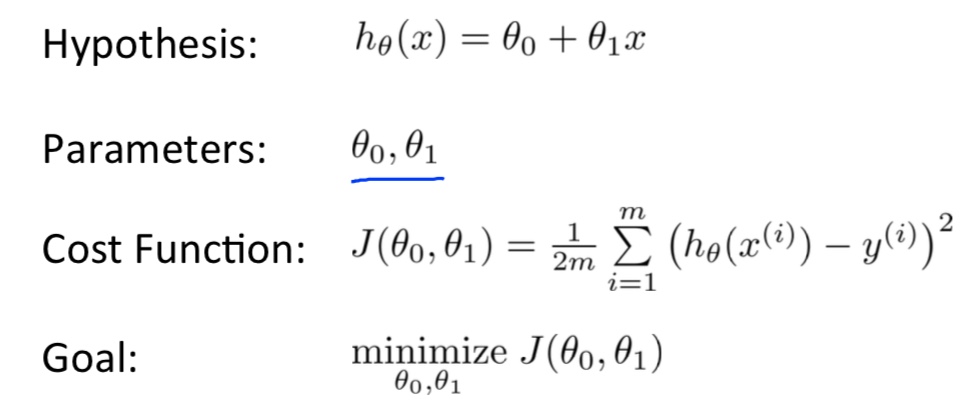基础
线性代数相关概念
- 对称矩阵:除对角线,其余值一三象限相等
- 对角矩阵(diagonal matrix):是一个主对角线之外的元素皆为0的矩阵
- 矩阵对角化:如果存在一个矩阵A,使$A^{-1}MA$ 的结果为对角矩阵,则称矩阵A将矩阵M 对角化。对于一个矩阵来说,不一定存在将其对角化的矩阵,但是任意一个n×n矩阵如果存在n个线性不相关的特征向量,则该矩阵可被对角化
- 定理(理解特征值和特征向量的作用):

- 定理(理解特征值和特征向量的作用):
- 实对称矩阵
- 实对称矩阵A的不同特征值对应的特征向量是正交的。(PCA算法最终就是将初始值的协方差矩阵变化为实对称矩阵)
- 实对称矩阵A的特征值都是实数,特征向量都是实向量。
协方差
- 均值描述的是样本集合的中间点,而标准差给我们描述的则是样本集合的各个样本点到均值的距离之平均,都是一维数据
$var(X)=\frac{\sum^{n}_{i=1}(X_i-\overline X)(X_i-\overline X)}{n}$ - 协方差:协方差就是这样一种用来度量两个随机变量关系的统计量
- $cov(X,Y)=\frac{\sum^{n}_{i=1}(X_i-\overline X)(Y_i-\overline Y)}{n}$。如果各维度均值都标准化为0,那么就简化为:$cov(X,Y)=\frac{\sum^{n}_{i=1}(X_i)(Y_i)}{n}$
- 如果结果为正值,则说明两者是正相关的,否则为负相关。如果为0,表示不相关,也就是正交
- 均值描述的是样本集合的中间点,而标准差给我们描述的则是样本集合的各个样本点到均值的距离之平均,都是一维数据
协方差矩阵
- 如果有多维的情况,就可以使用矩阵的思想来看更直观,比如三维的例子:
$C = \begin{bmatrix}
cov(x,x),cov(x,y),cov(x,z)
\
cov(y,x),cov(y,y),cov(y,z)
\
cov(z,x),cov(z,y),cov(z,z)
\end{bmatrix}$ - 协方差矩阵计算:
- 假设我们只有a和b两个字段(两维度特征),那么我们将它们按行组成矩阵X
$X=\begin{bmatrix}
a_1,a_2,a_3….a_n
\
b_1,b_2,b_3….b_n
\end{bmatrix}
$ - 然后我们用X乘以X的转置,并乘上系数1/m
$\frac1mXX^T=\begin{bmatrix}
\frac1m\sum^m_{i=1}a_ia_i \frac1m\sum^m_{i=1}a_ib_i
\
\frac1m\sum^m_{i=1}a_ib_i \frac1m\sum^m_{i=1}b_ib_i
\end{bmatrix}
$ - 设我们有m个n维数据记录,将其按列排成n乘m的矩阵X,设$C=1mXX𝖳,则C是一个对称矩阵,其对角线分别个各个字段的方差,而第i行j列和j行i列元素相同,表示i和j两个字段的协方差
- 假设我们只有a和b两个字段(两维度特征),那么我们将它们按行组成矩阵X
- 如果有多维的情况,就可以使用矩阵的思想来看更直观,比如三维的例子:




 所以:$y = \begin{bmatrix}
所以:$y = \begin{bmatrix}