层次聚类Louvain

发表于 | 分类于 ，

聚类总结

模块度

社区划分的标准–模块度
社区划分的标准–模块度2

  • 概念
    模块度（Modularity）用来衡量一个社区的划分是不是相对比较好的结果。一个相对好的结果在社区内部的节点相似度较高，而在社区外部节点的相似度较低
  • 定义
    社区内部的总边数和网络中总边数的比例减去一个期望值，该期望值是将网络设定为随机网络时同样的社区分配所形成的社区内部的总边数和网络中总边数的比例的大小
    • 公式一:
    • $k_v*k_w$,及随机网络的理解，可以参考
    • 公式二:
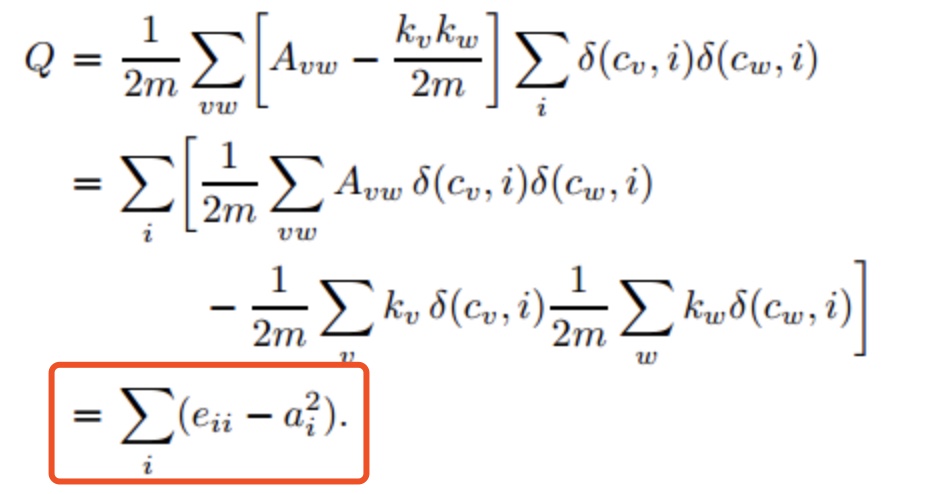
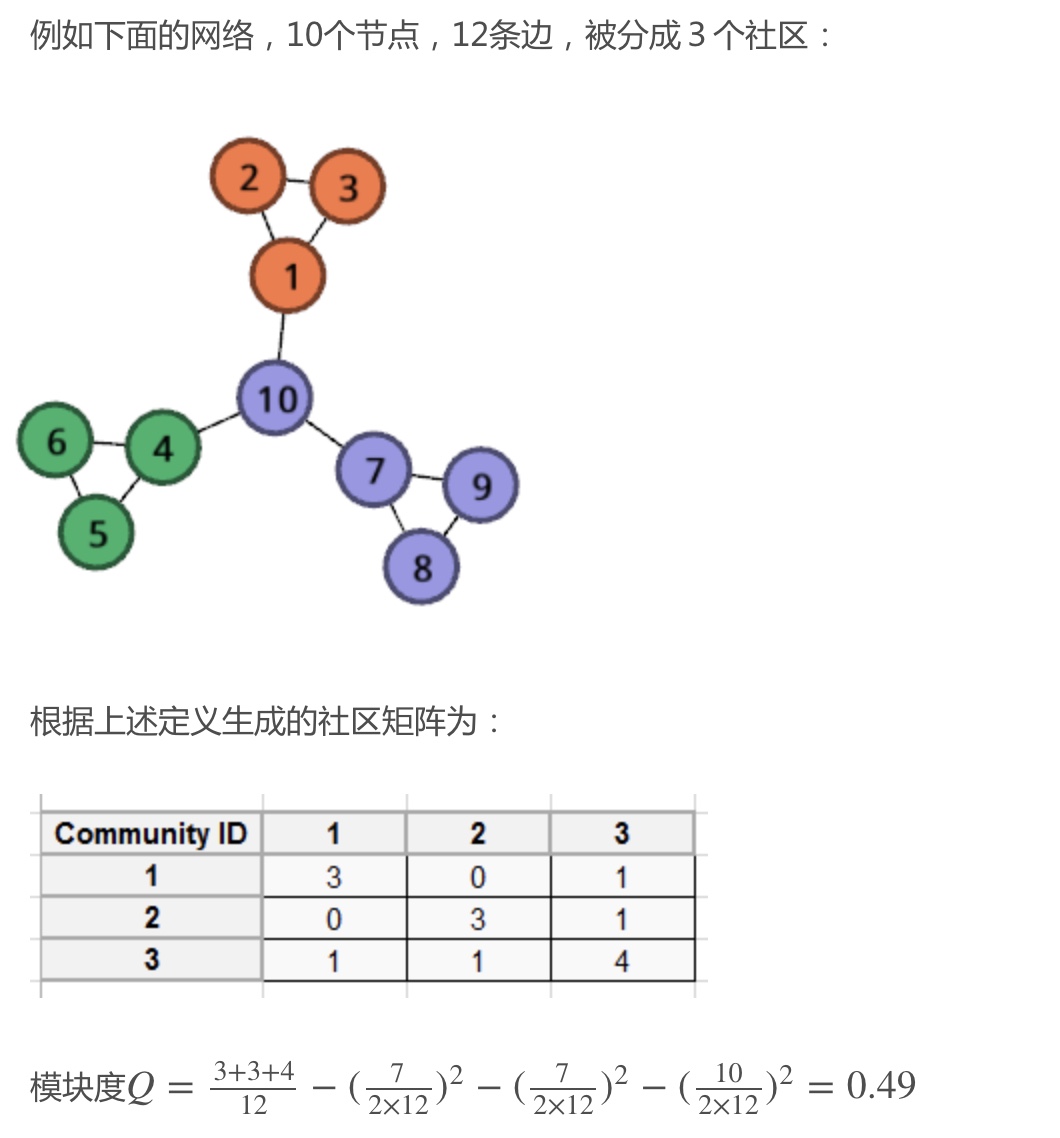
    • 举例：
      • 第一项是三项合在一起

Louvain算法

参考文章

  • Louvain算法是由底向上的层次聚类算法的一种，目的是优化提升模块度
  • 步骤
    • 1.将图中的每个节点看成一个独立的社区，次数社区的数目与节点个数相同；
    • 2.对每个节点i，依次尝试把节点i分配到其每个邻居节点所在的社区，计算分配前与分配后的模块度变化ΔQ，并记录ΔQ最大的那个邻居节点，如果maxΔQ>0，则把节点i分配ΔQ最大的那个邻居节点所在的社区，否则保持不变；
    • 3.重复2），直到所有节点的所属社区不再变化；
    • 4.对图进行压缩，将所有在同一个社区的节点压缩成一个新节点，社区内节点之间的边的权重转化为新节点的环的权重，社区间的边权重转化为新节点间的边权重；
    • 5.重复1）直到整个图的模块度不再发生变化