参考:
CF,FM,WDL,DeePFM算法对比总结
CTR模型演进
xDeepFM
- 背景
- 由上面的DCN网络可以看出:时间cross网络的每一层是上一层的乘以一个标量得到,并没有做到vector-wise的特征多阶交叉
- 特征交叉还是以deep部分的bit-wise的方式构建的
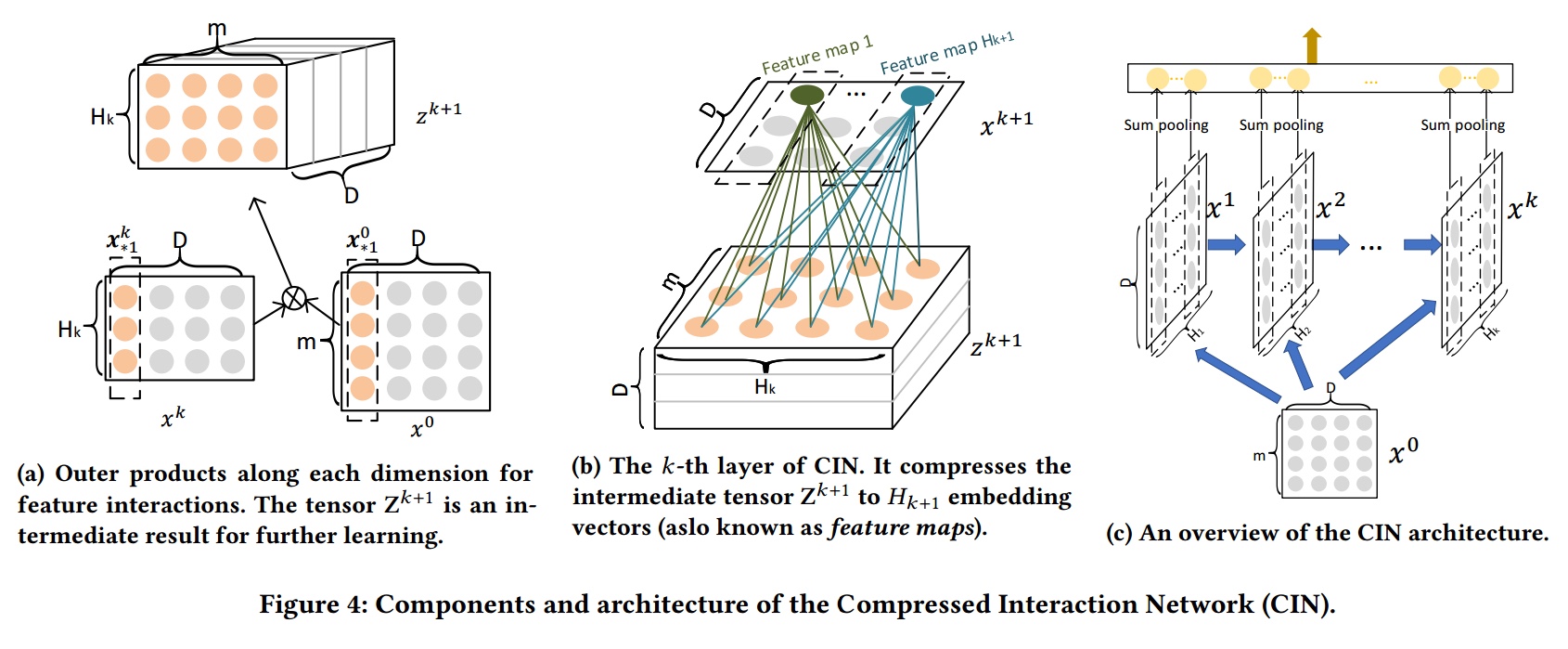
CIN网络(Compressed Interaction Network)
能够做到vector-wise基本的多阶特征交叉(outer product & 多阶:RNN网络思想),同时还能够进行维度控制(CNN网络中的池化思想)
- 概览
步骤1:
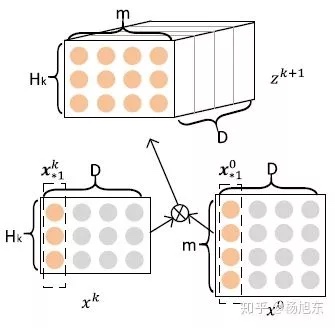
- 输入是所有field的embedding向量构成的矩阵$x^0 \in R^{m*D}$
- 该矩阵的第i行对应第个field的embedding向量,假设共有i个field,每个field的embedding向量的维度为D
- 输出:第k层的输出也是一个矩阵,记为$x^k \in R^{H_k*D}$
- 该矩阵的行数为$H_k$,表示第k层共有$H_k$个特征(embedding)向量,其中$H_0=m$,其他层不一定和m相等
- 第k层的输出$x^k$由第k-1层的输出$x^{k-1}$和$x_0$经过复杂(outer product)计算得到,具体的,矩阵$x^k$中的第h行的计算公式:
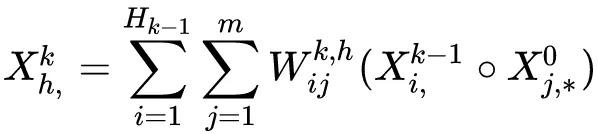
- 其中,0表示哈达玛积,即两个矩阵或向量对应元素相乘得到相同大小的矩阵或向量
- 输入是所有field的embedding向量构成的矩阵$x^0 \in R^{m*D}$
步骤二:
将步骤一种的多维m$H_k$D采用池化方法压缩成$H_k$*m维度向量,避免维度灾难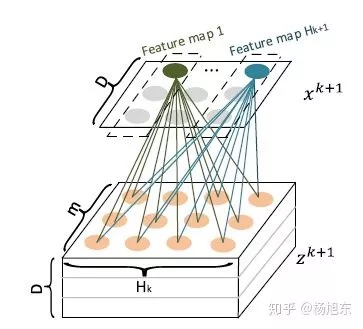
- $z^{k+1}$可以被看作是一个宽度为m、高度为$H_k$、通道数为 D 的图像,在这个虚拟的图像上施加一些卷积操作即得到$x^{k+1}$。$w^{k,h}$是其中一个卷积核,总共有$H_{k+1}$个不同的卷积核
步骤三:
$H_k$个feature再通过sum pooling,进行cat操作,连接得到不同交叉特征作为CIN的输出,这里也进行的降维CIN宏观
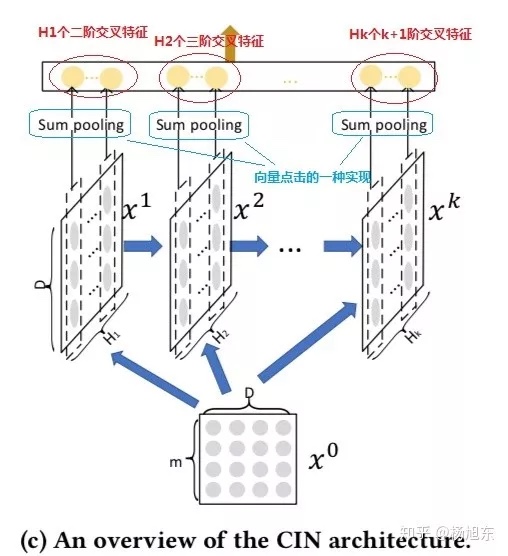
CIN的宏观框架如下图所示,它的特点是,最终学习出的特征交互的阶数是由网络的层数决定的,每一层隐层都通过一个池化操作连接到输出层,从而保证了输出单元可以见到不同阶数的特征交互模式。同时不难看出,CIN的结构与循环神经网络RNN是很类似的,即每一层的状态是由前一层隐层的值与一个额外的输入数据计算所得
- 不同的是,CIN中不同层的参数是不一样的,而在RNN中是相同的;RNN中每次额外的输入数据是不一样的,而CIN中额外的输入数据是固定的,始终是$x_0$
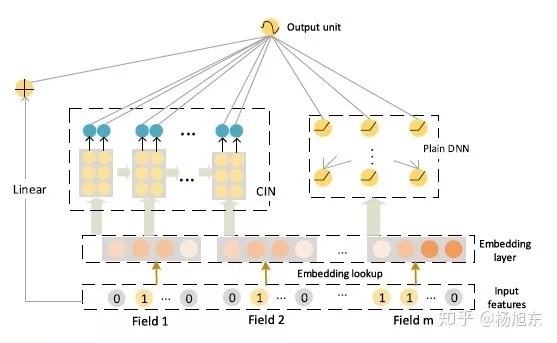
xDeepFM模型整体
借鉴Wide&Deep和DeepFM等模型的设计,将CIN与线性回归单元、全连接神经网络单元组合在一起,得到最终的模型并命名为极深因子分解机xDeepFM
- 特点:
既有线下模型的记忆能力,也集成了多维特征的显示交叉,同时也兼顾了DNN网络隐式特征交叉和泛华能力,在CIN网络也采用池化计算进行降维,有效的避免了维度爆炸的情况- CIN:集成显示的高阶特征交叉
- DNN:集成隐式的高阶特征交叉,并兼顾泛华能力
- 线下模型:集成线下模型有助于记忆功能